Performance evaluation of iterated extended Kalman filterwith variable step-length
介绍
优化方法主要基于最小化均方误差准则,对于线性高斯系统,导致了著名的卡尔曼滤波。与提供状态的条件PDF的贝叶斯方法不同,最优化方法提供状态的点估计和估计误差的相应协方差矩阵(CM)。与贝叶斯方法一样,基于最优化方法的状态估计问题只能在少数特殊情况下得到解析解。对于其他情况,估计方法通常遵循卡尔曼滤波框架,并利用非线性函数的线性化等逼近技术,例如,扩展(EKF)和二阶扩展卡尔曼滤波器[6]、[1]分别通过围绕当前估计到一阶或二阶的泰勒级数展开来逼近非线性函数,当线性化误差的影响往往会扰乱过滤的性能或其收敛性时,在更新状态附近重新线性化测量方程可能会减轻困难。
这种方法被称为迭代扩展卡尔曼过滤(IEKF)[6]。
IEKF计算状态估计不是作为近似条件平均值(就像EKF那样),而是作为最大后验(MAP)估计[7]。文献[8]证明了IEKF量测更新是高斯-牛顿(GN)方法的应用,而EKF是仅用一次GN方法迭代的IEKF的特例。
第二节简要介绍了EKF和IEKF的非线性状态估计及其求解方法。第三节简要介绍了IEKF的最新发展。第四节介绍了分析中使用的各种性能度量。接下来,在第五节中,通过两个数值例子对两种滤波器进行了比较,并在第六节中对本文进行了总结。
Nonlinear state estimation by EKF and IEKF
系统描述
离散时间非线性随机系统的状态空间形式如下:

其中,
向量\(\mathbf{x}_{k} \in \mathbb{R}^{n_{x}}\)和\(\mathbf{z}_{k} \in \mathbb{R}^{n_{z}}\)分别表示在时间k下,系统的状态和观测。
\(\mathbf{f}_{k}: \mathbb{R}^{n_{x}} \rightarrow \mathbb{R}^{n_{x}}\) and \(\mathbf{h}_{k}: \mathbb{R}^{n_{x}} \rightarrow \mathbb{R}^{n_{z}}\)是已知的向量函数。
\(\mathbf{w}_{k} \in \mathbb{R}^{n_{x}}\)和\(\mathbf{v}_{k} \in \mathbb{R}^{n_{z}}\)是相互独立的状态白噪声和测量白噪声。
噪声的概率密度函数是零均值且已知协方差矩阵\(\Sigma_{k}^{\mathbf{w}}\) and \(\Sigma_{k}^{\mathbf{v}}\)的高斯分布,即有\(p\left(\mathbf{w}_{k}\right)=\mathcal{N}\left\{\mathbf{w}_{k} ; \mathbf{0}_{n_{x} \times 1}, \Sigma_{k}^{\mathbf{w}}\right\} *\)和\(p\left(\mathbf{v}_{k}\right)=\mathcal{N}\left\{\mathbf{v}_{k} ; \mathbf{0}_{n_{z} \times 1}, \Sigma_{k}^{\mathbf{v}}\right\}\)。初始态的概率密度函数是高斯的,也是已知的,即\(p\left(\mathbf{x}_{0}\right)=\mathcal{N}\left\{\mathbf{x}_{0} ; \hat{\mathbf{x}}_{0}, \mathbf{P}_{0}\right\}\)。初始状态与噪声无关
扩展卡尔曼
最初,卡尔曼过滤是在1960年利用正交性原理[13]推导出来的。给出了具有线性函数\(\mathbf{f}_{k}\) and \(\mathbf{h}_{k}\)的系统(1)和(2)的最小均方误差估计。
对于非线性函数\(\mathbf{f}_{k}\) and \(\mathbf{h}_{k}\),必须使用近似,例如在EKF中使用的近似。EKF基于一阶泰勒级数展开(TE1)。在假设状态预测平均值\(\hat{\mathbf{x}}_{k \mid k-1}=\mathrm{E}\left[\mathbf{x}_{k} \mid \mathbf{z}^{k-1}\right]\)(定义线性化点)已知的条件下,函数\(\mathbf{h}_{k}\)的泰勒一阶展开由下式给出:
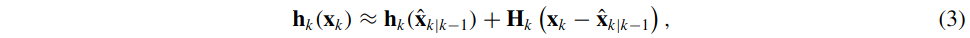
其中,矩阵\(\mathbf{H}_{k}=\left.\frac{\partial \mathbf{h}\left(\mathbf{x}_{k}\right)}{\partial \mathbf{x}_{k}}\right|_{\mathbf{x}_{k}=\hat{\mathbf{x}}_{k \mid k-1}}\)是测量函数\(\mathbf{h}_{k}(\cdot)\)关于\(\mathbf{X}_{k}\)在线性化点\(\hat{\mathbf{X}}_{k \mid k-1}\)的雅可比。
预测更新步骤的TE1近似的使用是类似的。在已知滤波均值\(\hat{\mathbf{x}}_{k \mid k}=\mathrm{E}\left[\mathbf{x}_{k} \mid \mathbf{z}^{k}\right]\)的假设下,(1)中的\(\mathbf{f}_{k}\)的TE1具有如下形式:

其中,\(\mathbf{F}_{k}=\left.\frac{\partial \mathbf{f}\left(\mathbf{x}_{k}\right)}{\partial \mathbf{x}_{k}}\right|_{\mathbf{x}_{k}=\hat{\mathbf{x}}_{k \mid k}}\)是系统矩阵\(\mathbf{f}_{k}(\cdot)\)关于关于\(\mathbf{X}_{k}\)在线性化点\(\hat{\mathbf{X}}_{k \mid k}\)的雅可比。
扩展卡尔曼算法如下:

对于具有轻度非线性函数\(\mathbf{f}_{k}\) and \(\mathbf{h}_{k}\)的系统,扩展卡尔曼滤波性能良好,但是如果测量方程(2)是强非线性的(例如在纯方位跟踪问题中),滤波器的性能就会恶化。在这种情况下,IEKF往往比EKF提供更准确的估计。
迭代扩展卡尔曼
IEKF[6]的想法是在存在显著非线性的情况下改进参考轨迹,从而改进估计。这些改进是通过EKF测量更新的局部迭代实现的(参见算法2)。迭代通常在连续迭代中没有显著变化或满足其他标准(如最大迭代次数)时停止。算法如下:



翻译一下,就是以下步骤:
初始化:设置迭代次数\(i=0\),此时有\(\hat{\mathbf{x}}_{k}^{0}=\hat{\mathbf{x}}_{k \mid k-1}\),表示在第k次观测的第0次迭代的状态\(\mathbf{x}_{k}^{0}\)等于利用前\(k-1\)次观测以及所预测的k时刻的状态\(\hat{\mathbf{X}}_{k \mid k-1}\)
测量更新:计算测量函数在迭代状态\(\mathbf{x}_{k}^{i}\)处的雅可比\(\mathbf{H}_{k}^{i}\),更新第i次迭代的卡尔曼增益\(\mathbf{K}_{k}^{i}\),更新第i次迭代后的状态\(\hat{\mathbf{x}}_{k}^{i+1}\),如下:

其中,
\(\mathbf{H}_{k}^{i}\)是测量函数在迭代状态\(\mathbf{x}_{k}^{i}\)处
\(\mathbf{P}_{k \mid k-1}\)是利用前\(k-1\)次观测以及所预测的k时刻的协方差,即第0次迭代前的协方差
\(\hat{\mathbf{x}}_{k \mid k-1}\)是利用前\(k-1\)次观测以及所预测的k时刻的状态,即第0次迭代前的状态
\(\hat{\mathbf{x}}_{k}^{i}\)是第k观测下,迭代i次后的状态
\(\hat{\mathbf{x}}_{k}^{i+1}\)是第k观测下,迭代i+1次后的状态
- 迭代完成后,需要更新(保存)状态和协方差:
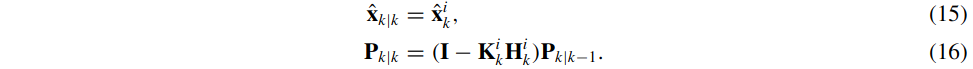
即协方差是在迭代结束后再更新的,迭代过中一直使用的是\(\mathbf{P}_{k \mid k-1}\),即上一次更新完后又预测到k时刻的协方差。
值得一提的是,即使在IEKF算法中发生的重新线性化也不能保证滤波器的收敛性,IEKF也不总是比扩展卡尔曼滤波性能好。不过,IEKF测量更新有两个非常有趣的属性:
它可以看作是高斯-牛顿法的一种应用
它生成最大后验(MAP)估计:\(\hat{\mathbf{x}}_{k \mid k}^{\mathrm{MAP}}=\underset{\mathbf{x}_{k}}{\arg \max } p\left(\mathbf{x}_{k} \mid \mathbf{z}^{k}\right)\)
对迭代扩展卡尔曼过滤算法的改进
如上所述,IEKF可以看作是求解非线性最小二乘问题的GN方法的一种应用。因此,在IEKF中可以使用对GN方法的改进来提高方法的性能和收敛性,以提高估计的质量。改变步长是常用的改进措施之一。首先,介绍了IEKF最小化的MAP准则。
MAP criterion
如果使用系统(1)和(2)的概率描述,则使用先验的概率密度函数\(p\left(\mathbf{x}_{k} \mid \mathbf{z}^{k-1}\right)\)来求后验PDF\(p\left(\mathbf{x}_{k} \mid \mathbf{z}^{k}\right)\)。
先验的概率分布\(p\left(\mathbf{x}_{k} \mid \mathbf{z}^{k-1}\right)\)的均值\(\hat{\mathbf{X}}_{k \mid k-1}\)和协方差\(\mathbf{P}_{k \mid k-1}\)在算法1的时间更新步骤中计算。其假设为高斯,并且在算法2的测量更新中计算后验PDF\(p\left(\mathbf{x}_{k} \mid \mathbf{z}^{k-1}\right)\)的均值\(\hat{\mathbf{x}}_{k \mid k}\)和方差\(\mathbf{P}_{k \mid k}\)。
后验概率\(p\left(\mathbf{x}_{k} \mid \mathbf{z}^{k}\right)\)与似然\(p\left(\mathbf{z}_{k} \mid \mathbf{x}_{k}\right)=p_{\mathbf{v}_{k}}\left(\mathbf{z}_{k}-\mathbf{h}_{k}\left(\mathbf{x}_{k}\right)\right)\)与先验\(p\left(\mathbf{x}_{k} \mid \mathbf{z}^{k-1}\right)\)的乘积成正比,即有:
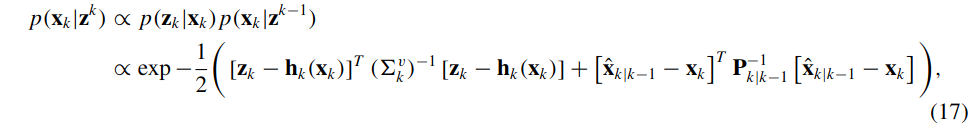
其中,为方便起见,不依赖于\(\mathbf{X}_{k}\)的项已被删除。然后由下式给出MAP估计:

现在,有了MAP模型,可以使用GN方法来找到\(\hat{\mathbf{x}}_{k \mid k}\),以达到最小化函数。理想情况下,每次GN方法迭代(即IEKF测量更新迭代)都应该减小准则\(\mathbf{V}_{k}\)。
IEKF测量更新(16)可以用隐式方式被重写:
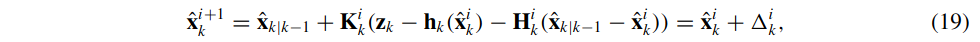
本次迭代更新偏移量\(\Delta_{k}^{i}\)如下:
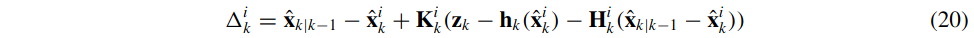
其中,\(\hat{\mathbf{x}}_{k}^{0}=\hat{\mathbf{x}}_{k \mid k-1}\),即在第k次观测的第0次迭代的状态\(\mathbf{x}_{k}^{0}\)等于利用前\(k-1\)次观测以及所预测的k时刻的状态\(\hat{\mathbf{X}}_{k \mid k-1}\)(先验)
对于高斯牛顿方法,也可以求出更新偏移量\(\Delta_{k}^{i}\)的另一种表达形式:
高斯牛顿法就是将\(f(\mathbf{x})\)进行一届泰勒展开(注意这里的\(f(\mathbf{x})\)不是目标函数,而是原函数,即\(f(\mathbf{x}) = z-h(\mathbf{x})\)
因此,有:
\[ f(\mathbf{x}+\Delta{\mathbf{x}}) \approx f(\mathbf{x}) + \mathbf{J}(\mathbf{x})\Delta{\mathbf{x}} \]
其中,\(\mathbf{J}(\mathbf{x})\)为\(f(\mathbf{x})\)关于\(\mathbf{x}\)的雅克比。
经过系列变换,最终可以得到正规方程:
\[ \mathbf{J}(\mathbf{x})^{T}\mathbf{J}(\mathbf{x}) \Delta{\mathbf{x}} = -\mathbf{J}(\mathbf{x})^{T} f(\mathbf{x}) \]
因此有:
\[ \Delta{\mathbf{x}} = - \left (\mathbf{J}(\mathbf{x})^{T}\mathbf{J}(\mathbf{x})\right)^{-1} \mathbf{J}(\mathbf{x})^{T} f(\mathbf{x}) \]
对于式(17)(18)所展示的MAP问题,可以进一步建模为:
\[ \begin{aligned} \hat{\mathbf{x}}_{k \mid k} &=\underset{\mathbf{x}_{k}}{\arg \min } \frac{1}{2}\left(\left[\mathbf{z}_{k}-\mathbf{h}_{k}\left(\mathbf{x}_{k}\right)\right]^{T}\left(\Sigma_{k}^{v}\right)^{-1}\left[\mathbf{z}_{k}-\mathbf{h}_{k}\left(\mathbf{x}_{k}\right)\right]+\left[\hat{\mathbf{x}}_{k \mid k-1}-\mathbf{x}_{k}\right]^{T} \mathbf{P}_{k \mid k-1}^{-1}\left[\hat{\mathbf{x}}_{k \mid k-1}-\mathbf{x}_{k}\right]\right) \\ &=\underset{\mathbf{x}_{k}}{\arg \min } \frac{1}{2} r(\mathbf{X})^{T}r(\mathbf{X}) \end{aligned} \]
其中,
\[ r(\mathbf{X})=\left[\begin{array}{c} \left(\mathbf{R}_{k}\right)^{-\frac{1}{2}}(\mathbf{z}_k-h(\mathbf{x}_k)) \\ \mathbf{P}_{k \mid k-1}^{-\frac{1}{2}}\left(\hat{\mathbf{x}}_{k \mid k-1}- \mathbf{x}_k \right) \end{array}\right] \]
雅克比\(J(\mathbf{X})\)如下:
\[ \mathbf{J}_{k}=-\left[\begin{array}{c} \mathbf{R}_{k}^{-1 / 2} \mathbf{H}_{k} \\ \mathbf{P}_{k \mid k-1}^{-1 / 2} \end{array}\right] \]
\[ \mathbf{H}_{k}=\left.\frac{\partial h(s)}{\partial s}\right|_{s=\mathbf{x}_{k}} \]
将信息回代到高斯牛顿正规方程,可以得到增量\(\Delta{\mathbf{x}}\)如下:
\[ \begin{aligned} \Delta{\mathbf{x}} &= - \left (\mathbf{J}(\mathbf{x})^{T}\mathbf{J}(\mathbf{x})\right)^{-1} \mathbf{J}(\mathbf{x})^{T} f(\mathbf{x}) \\ &= \left( \left[\begin{array}{c} \mathbf{R}_{k}^{-1 / 2} \mathbf{H}_{k} \\ \mathbf{P}_{k \mid k-1}^{-1 / 2} \end{array}\right]^{T} \left[\begin{array}{c} \mathbf{R}_{k}^{-1 / 2} \mathbf{H}_{k} \\ \mathbf{P}_{k \mid k-1}^{-1 / 2} \end{array}\right] \right)^{-1} \left[\begin{array}{c} \mathbf{R}_{k}^{-1 / 2} \mathbf{H}_{k} \\ \mathbf{P}_{k \mid k-1}^{-1 / 2} \end{array}\right]^{T} \left[\begin{array}{c} \left(\mathbf{R}_{k}\right)^{-\frac{1}{2}}(\mathbf{z}_k-h(\mathbf{x}_k)) \\ \mathbf{P}_{k \mid k-1}^{-\frac{1}{2}}\left(\hat{\mathbf{x}}_{k \mid k-1}- \mathbf{x}_k \right) \end{array}\right]\\ &= \left( \mathbf{H}_k^{T} \mathbf{R}_k^{-1} \mathbf{H}_k + \mathbf{P}_k^{-1} \right)^{-1} \left( \mathbf{H}_k^{T} \mathbf{R}_k^{-1} (\mathbf{z}_k-h(\mathbf{x}_k)) + \mathbf{P}_k^{-1}(\hat{\mathbf{x}}_{k \mid k-1}- \mathbf{x}_k) \right) \\ &= \left( \mathbf{H}_k^{T} \mathbf{R}_k^{-1} \mathbf{H}_k + \mathbf{P}_k^{-1} \right)^{-1} \{ \mathbf{H}_k^{T} \mathbf{R}_k^{-1} (\mathbf{z}_k-h(\mathbf{x}_k) - \mathbf{H}_k (\hat{\mathbf{x}}_{k \mid k-1}- \mathbf{x}_k)) + \\ & \mathbf{H}_k^{T} \mathbf{R}_k^{-1} \mathbf{H}_k (\hat{\mathbf{x}}_{k \mid k-1}- \mathbf{x}_k) + \mathbf{P}_k^{-1}(\hat{\mathbf{x}}_{k \mid k-1}- \mathbf{x}_k) \} \\ &= \hat{\mathbf{x}}_{k \mid k-1}- \mathbf{x}_k + \left( \mathbf{H}_k^{T} \mathbf{R}_k^{-1} \mathbf{H}_k + \mathbf{P}_k^{-1} \right)^{-1} \mathbf{H}_k^{T} \mathbf{R}_k^{-1} \left ( \mathbf{z}_k-h(\mathbf{x}_k) - \mathbf{H}_k (\hat{\mathbf{x}}_{k \mid k-1}- \mathbf{x}_k) \right) \end{aligned} \]
此时,如果令\(\mathbf{K}_{k}\)满足:
\[\mathbf{K}_{k} = \left( \mathbf{H}_k^{T} \mathbf{R}_k^{-1} \mathbf{H}_k + \mathbf{P}_k^{-1} \right)^{-1} \mathbf{H}_k^{T} \mathbf{R}_k^{-1} \]
定睛一看,这货不就是公式(20)由IEKF的增量吗?
所以,IEKF实际上是高斯牛顿的一种应用,如果多个观测放在一起来求解,就是最小二乘,如果迭代的求解,就成了IEKF。
IEKF在Fast-LIO系列的应用
回顾Fast-LIO1论文,公式(17),要优化的目标函数是:

其中,包含了先验项和观测项
先验项
- 第一项\(\left\|\mathbf{x}_{k} \boxminus \widehat{\mathbf{x}}_{k}\right\|_{\widehat{\mathbf{P}}_{k}^{-1}}^{2}\)是先验项,其表述有点奇怪
原文描述如下:
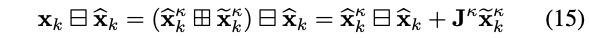
其中,
- \(\mathbf{X}_{k}\)表示状态真值
- \(\widehat{\mathbf{x}}_{k}\)表示k时刻预测值
- \(\mathbf{J}^{\kappa}\)表示\(\left(\widehat{\mathbf{x}}_{k}^{\kappa} \boxplus \widetilde{\mathbf{x}}_{k}^{\kappa}\right) \boxminus \widehat{\mathbf{x}}_{k}\)关于误差状态\(\tilde{\mathbf{x}}_{k}^{\kappa}\)的雅克比
按照原文的意思是,\(\left\|\mathbf{x}_{k} \boxminus \widehat{\mathbf{x}}_{k}\right\|_{\widehat{\mathbf{P}}_{k}^{-1}}^{2}\)用于约束预测值\(\widehat{\mathbf{x}}_{k}\)不应该离状态真值太远,即误差状态应尽可能小(这个先验看起来跟平时的形式不一样,难以理解)。
下面,按照我们通用的理解去描述:
先验一般约束着迭代状态值\(\widehat{\mathbf{x}}_{k}^{\kappa}\)不应该离预测值\(\widehat{\mathbf{x}}_{k}\)太远,因此,先验对应的残差项可以写为:
\[ \widehat{\mathbf{x}}_{k}^{\kappa} \boxminus \widehat{\mathbf{x}}_{k} \]
因此,个人认为,原文公式(17)第一项不应该为\(\mathbf{x}_{k} \boxminus \widehat{\mathbf{x}}_{k}\),替换为\(\widehat{\mathbf{x}}_{k}^{\kappa} \boxminus \widehat{\mathbf{x}}_{k}\)更合理
观测项
- 第二项\(\left\|\mathbf{z}_{j}^{\kappa}+\mathbf{H}_{j}^{\kappa} \widetilde{\mathbf{x}}_{k}^{\kappa}\right\|_{\mathbf{R}_{j}^{-1}}^{2}\)在原文中的表述比较牵强:
原文公式如下:
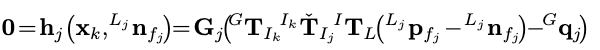
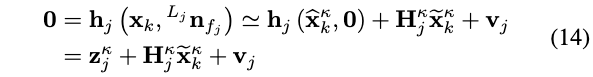
上面\(\mathbf{h}_{j}\left(\mathbf{x}_{k},{ }^{L_{j}} \mathbf{n}_{f_{j}}\right)\)的意思是,给定状态真值\(\mathbf{x}_{k}\)和测量噪声\({ }^{L_{j}} \mathbf{n}_{f_{j}}\),那么理论上得到的观测值(即点到平面的距离)为0。
然而,由于无法得知状态真值,因此使用一阶近似得到的公式(14)。此处使用的\(\mathbf{z}_{j}^{\kappa}+\mathbf{H}_{j}^{\kappa} \widetilde{\mathbf{x}}_{k}^{\kappa}\)让人容易混淆,还是看下文的另外一种描述。
前面提到,实际的观测值其实不用去观测,因为点就在平面上,所以实际的观测值为0,即\(\mathbf{z_{true}} = 0\)。
为了衡量当前估计的状态是否足够接近真值,我们利用迭代的状态去计算点-面距离,这一个操作称为观测预测,\(\mathbf{h}_{j}\left(\widehat{\mathbf{x}}_{k}^{\kappa}, \mathbf{0}\right)\)为观测预测模型,即通过给定状态来计算在该状态下得到的观测值,此处为计算得到的点-面距离。
因此,残差项可以写为:
\[ \mathbf{z_{true}} -\mathbf{h}_{j}\left(\widehat{\mathbf{x}}_{k}^{\kappa}, \mathbf{0}\right) \]
其中,已知\(\mathbf{z_{true}} = 0\),因此,残差项就是利用迭代的状态计算得到的点-面距离\(\mathbf{h}_{j}\left(\widehat{\mathbf{x}}_{k}^{\kappa}\right)\)。
因此,个人认为,原文描述的第二项不应该为\(\left\|\mathbf{z}_{j}^{\kappa}+\mathbf{H}_{j}^{\kappa} \widetilde{\mathbf{x}}_{k}^{\kappa}\right\|_{\mathbf{R}_{j}^{-1}}^{2}\),替换为\(\left\| \mathbf{z_{true}} -\mathbf{h}_{j}\left(\widehat{\mathbf{x}}_{k}^{\kappa}, \mathbf{0}\right)\right\|_{\mathbf{R}_{j}^{-1}}^{2} = \left\|\mathbf{h}_{j}\left(\widehat{\mathbf{x}}_{k}^{\kappa}, \mathbf{0}\right)\right\|_{\mathbf{R}_{j}^{-1}}^{2}\)更为合适。
推导
综上,我们继续使用上面的方法再一次推导:
假设目标函数\(r(\mathbf{X})\)如下:
\[ r(\mathbf{X})=\left[\begin{array}{c} \left(\mathbf{R}_{k}\right)^{-\frac{1}{2}}\left ( \mathbf{z_{true}} -\mathbf{h}_{j}(\widehat{\mathbf{x}}_{k}^{\kappa}, \mathbf{0}) \right) \\ \mathbf{P}_{k \mid k-1}^{-\frac{1}{2}}\left(\mathbf{x}_{k} \boxminus \widehat{\mathbf{x}}_{k} \right) \end{array}\right] = \left[\begin{array}{c} \left(\mathbf{R}_{k}\right)^{-\frac{1}{2}}\left ( \mathbf{h}_{j}(\widehat{\mathbf{x}}_{k}^{\kappa}, \mathbf{0}) \right) \\ \mathbf{P}_{k \mid k-1}^{-\frac{1}{2}}\left(\mathbf{x}_{k} \boxminus \widehat{\mathbf{x}}_{k} \right) \end{array}\right] \]
其中,
- \(\mathbf{h}_{j}\left(\widehat{\mathbf{x}}_{k}^{\kappa}, \mathbf{0}\right)\)是观测模型,对其进行泰勒一阶展开,可得:\(\mathbf{h}_{j}\left(\widehat{\mathbf{x}}_{k}^{\kappa}\boxplus\tilde{\mathbf{x}}_{k}^{\kappa}, \mathbf{0}\right) \approx \mathbf{z}_{j}^{\kappa}+\mathbf{H}_{j}^{\kappa} \tilde{\mathbf{x}}_{k}^{\kappa}\),其中\(\mathbf{z}_{j}^{\kappa}\)就是利用状态\(\widehat{\mathbf{X}}_{k}^{\kappa}\)计算得到的点到平面距离
- \(j\)表示第j个激光点
根据高斯牛顿的思想,对残差函数进行一阶泰勒展开如下:
\[ \begin{aligned} r(\mathbf{X^{\kappa} +\Delta \mathbf{x}}) = r(\mathbf{X^{\kappa} +\tilde{\mathbf{x}}_{k}^{\kappa}}) &= r(\mathbf{X^{\kappa}})+ J(\mathbf{X}^{\kappa})\tilde{\mathbf{x}}_{k}^{\kappa} \\ &= \left[\begin{array}{c} \left(\mathbf{R}_{k}\right)^{-\frac{1}{2}}(\mathbf{z}_{j}^{\kappa}+\mathbf{H}_{j}^{\kappa} \tilde{\mathbf{x}}_{k}^{\kappa}) \\ \mathbf{P}_{k \mid k-1}^{-\frac{1}{2}}\left(\widehat{\mathbf{x}}_{k}^{\kappa} \boxminus \widehat{\mathbf{x}}_{k}+\mathbf{J}^{\kappa} \widetilde{\mathbf{x}}_{k}^{\kappa}\right) \end{array}\right] \\ &= \left[\begin{array}{c} \left(\mathbf{R}_{k}\right)^{-\frac{1}{2}}(\mathbf{z}_{j}^{\kappa}) \\ \mathbf{P}_{k \mid k-1}^{-\frac{1}{2}}\left(\widehat{\mathbf{x}}_{k}^{\kappa} \boxminus \widehat{\mathbf{x}}_{k}\right) \end{array}\right] + \left[\begin{array}{c} \left(\mathbf{R}_{k}\right)^{-\frac{1}{2}}(\mathbf{H}_{j}^{\kappa}) \\ \mathbf{P}_{k \mid k-1}^{-\frac{1}{2}}\left(\mathbf{J}^{\kappa} \right) \end{array}\right] \widetilde{\mathbf{x}}_{k}^{\kappa} \end{aligned} \]
其中
- \(\mathbf{H}^{\kappa}_{j}\)是激光投影点到地图上最近的平面的距离关于误差状态的雅克比,其推导可从R2LIVE中找到。
- \(\mathbf{J}^{\kappa}\)表示\(\widehat{\mathbf{x}}_{k}^{\kappa} \boxminus \widehat{\mathbf{x}}_{k}\)关于误差状态\(\tilde{\mathbf{x}}_{k}^{\kappa}\)的雅克比
雅克比\(J(\mathbf{X}^{\kappa})\)如下:
\[ \mathbf{J}_{k}^{\kappa} =\left[\begin{array}{c} \mathbf{R}_{k}^{-1 / 2} \mathbf{H}_{k}^{\kappa} \\ \mathbf{P}_{k \mid k-1}^{-1 / 2} \mathbf{J}^{\kappa} \end{array}\right] \]
\[ \mathbf{H}_{k}^{\kappa} =\left.\frac{\partial h(s)}{\partial s}\right|_{s=\mathbf{x}_{k}^{\kappa} } \]
\[ \mathbf{J}^{\kappa}=\left[\begin{array}{cc} \mathbf{A}\left({ }^{G} \widehat{\mathbf{R}}_{I_{k}}^{\kappa} \boxminus^{G} \widehat{\mathbf{R}}_{I_{k}}\right)^{-T} & \mathbf{0}_{3 \times 15} \\ \mathbf{0}_{15 \times 3} & \mathbf{I}_{15 \times 15} \end{array}\right] \]
这里注意区分\(\mathbf{J}_{k}\)和\(\mathbf{J}^{\kappa}\)。
将\(r(\mathbf{X^{\kappa}})\)以及雅克比\(J(\mathbf{X}^{\kappa})\)回代到高斯牛顿正规方程,可以得到增量\(\Delta{\mathbf{x}}\)如下:
\[ \begin{aligned} \Delta{\mathbf{x}} &= - \left (\mathbf{J}(\mathbf{x})^{T}\mathbf{J}(\mathbf{x})\right)^{-1} \mathbf{J}(\mathbf{x})^{T} f(\mathbf{x}) \\ &= - \left( \left[\begin{array}{c} \mathbf{R}_{k}^{-1 / 2} \mathbf{H}_{k}^{\kappa} \\ \mathbf{P}_{k \mid k-1}^{-1 / 2} \mathbf{J}^{\kappa} \end{array}\right]^{T} \left[\begin{array}{c} \mathbf{R}_{k}^{-1 / 2} \mathbf{H}_{k}^{\kappa} \\ \mathbf{P}_{k \mid k-1}^{-1 / 2} \mathbf{J}^{\kappa} \end{array}\right] \right)^{-1} \left[\begin{array}{c} \mathbf{R}_{k}^{-1 / 2} \mathbf{H}_{k}^{\kappa} \\ \mathbf{P}_{k \mid k-1}^{-1 / 2} \mathbf{J}^{\kappa} \end{array}\right]^{T} \left[\begin{array}{c} \left(\mathbf{R}_{k}\right)^{-\frac{1}{2}}(\mathbf{z}_{j}^{\kappa}) \\ \mathbf{P}_{k \mid k-1}^{-\frac{1}{2}}\left(\widehat{\mathbf{x}}_{k}^{\kappa} \boxminus \widehat{\mathbf{x}}_{k}\right) \end{array}\right] \\ &= - \left( \mathbf{H}_k^{T} \mathbf{R}_k^{-1} \mathbf{H}_k + (\mathbf{J}^{\kappa})^{T}\mathbf{P}_k^{-1}(\mathbf{J}^{\kappa}) \right)^{-1} \left \{ \mathbf{H}_k^{T} \mathbf{R}_k^{-1} \mathbf{z}_k^{\kappa} + (\mathbf{J}^{\kappa})^{T}\mathbf{P}_k^{-1} \left(\widehat{\mathbf{x}}_{k}^{\kappa} \boxminus \widehat{\mathbf{x}}_{k}\right) \right \} \\ &= - \left( \mathbf{H}_k^{T} \mathbf{R}_k^{-1} \mathbf{H}_k + (\mathbf{J}^{\kappa})^{T}\mathbf{P}_k^{-1}(\mathbf{J}^{\kappa}) \right)^{-1} \{ \mathbf{H}_k^{T} \mathbf{R}_k^{-1} \mathbf{z}_k^{\kappa} + (\mathbf{J}^{\kappa})^{T}\mathbf{P}_k^{-1}(\mathbf{J}^{\kappa})(\mathbf{J}^{\kappa})^{-1} \left(\widehat{\mathbf{x}}_{k}^{\kappa} \boxminus \widehat{\mathbf{x}}_{k}\right) \\ &+ \mathbf{H}_k^{T} \mathbf{R}_k^{-1} \mathbf{H}_k (\mathbf{J}^{\kappa})^{-1} \left(\widehat{\mathbf{x}}_{k}^{\kappa} \boxminus \widehat{\mathbf{x}}_{k}\right) - \mathbf{H}_k^{T} \mathbf{R}_k^{-1} \mathbf{H}_k (\mathbf{J}^{\kappa})^{-1} \left(\widehat{\mathbf{x}}_{k}^{\kappa} \boxminus \widehat{\mathbf{x}}_{k}\right) \} \\ &= -(\mathbf{J}^{\kappa})^{-1} \left(\widehat{\mathbf{x}}_{k}^{\kappa} \boxminus \widehat{\mathbf{x}}_{k}\right) - \left( \mathbf{H}_k^{T} \mathbf{R}_k^{-1} \mathbf{H}_k + (\mathbf{J}^{\kappa})^{T}\mathbf{P}_k^{-1}(\mathbf{J}^{\kappa}) \right)^{-1} (\mathbf{H}_k^{T} \mathbf{R}_k^{-1}) \left ( \mathbf{z}_k^{\kappa} + \mathbf{H}_k(\mathbf{J}^{\kappa})^{-1} \left(\widehat{\mathbf{x}}_{k}^{\kappa} \boxminus \widehat{\mathbf{x}}_{k}\right) \right ) \\ &= -(\mathbf{J}^{\kappa})^{-1} \left(\widehat{\mathbf{x}}_{k}^{\kappa} \boxminus \widehat{\mathbf{x}}_{k}\right) - \mathbf{K}_{k}^{\kappa} \left ( \mathbf{z}_k^{\kappa} + \mathbf{H}_k(\mathbf{J}^{\kappa})^{-1} \left(\widehat{\mathbf{x}}_{k}^{\kappa} \boxminus \widehat{\mathbf{x}}_{k}\right) \right ) \\ &= -\mathbf{K} \mathbf{z}_{k}^{\kappa}-(\mathbf{I}-\mathbf{K} \mathbf{H})\left(\mathbf{J}^{\kappa}\right)^{-1}\left(\widehat{\mathbf{x}}_{k}^{\kappa} \boxminus \widehat{\mathbf{x}}_{k}\right) \end{aligned} \]
按照上述推导,即可得到与论文公式(18)一致的结果。
参考
论文:Performance evaluation of iterated extended Kalman filter with variable step-length