Robust and Online LiDAR-inertial Initialization

介绍
摘要:对于大多数LiDAR惯性里程计来说,精确的初始状态,包括时间偏差和LiDAR与6轴IMU之间的外参,起着重要的作用,通常被认为是前提条件。然而,在定制的激光雷达惯性系统中,这样的信息并不总是可用的,本文提出了一种完全在线的激光雷达惯性系统初始化过程,该过程通过校准激光雷达和IMU之间的时间偏差和外参,并通过将激光雷达测量的状态估计值与IMU测量的状态值对齐来校正重力矢量和IMU偏差。我们将所提出的方法实现为一个初始化模块,如果启用该模块,它将自动检测采集数据的激发程度,同时校准时间偏移量、外参偏移量、重力矢量和惯性测量单元偏差,然后将其用作在线激光雷达惯性里程仪系统的高质量初始状态值。对不同类型的激光雷达和激光雷达-惯性组合进行的实验表明了该初始化方法的鲁棒性、适应性和有效性。
我们的LiDAR-惯性初始化法的主要目的之一是在没有任何初始估计的情况下校准LiDAR和IMU之间的外特性。现有的一些外部标定方法是基于批量优化的,数据关联性很强,耗时较大。例如,Lveal。[14]提出了一种基于连续时间批优化的标定方法。B样条的使用使得需要估计的参数较多,计算量也较大。[15]使用扩展卡尔曼过滤估计运动补偿复杂的外域变换,收敛速度有限。与这些方法相比,我们的方法更轻量级,能够快速运行,同时仍然可以获得足够精确的外部校准,以便后续的在线估计(例如,通过[1])。我们的方法还校准了[14,15]中没有考虑的时间偏移。此外,文献[14,15]所采用的基于NDT的扫描-扫描匹配通常不适用于具有非重复扫描模式的激光雷达。相比之下,我们的方法采用了扫描到地图的匹配策略,可以很容易地应用重复扫描和非重复扫描的LiDAR。
方法
系统框架
由于IMU只有在运动时才被激发[15],所以我们的初始化过程是基于运动的方法,这意味着充分的激励是必要的。我们工作流程的概述如图2所示,一些重要符号如表一所示。我们建议的LiDAR里程计(参见第III-B节)由FAST-LIO2[1]改进而来,采用恒定(角和线)速度(CV)模型来预测LiDAR运动并进行畸变矫正。
为了缓解恒速模型与传感器实际运动之间的失配,通过将输入帧分割成几个子帧来提高LiDAR里程计速率。
如果LiDAR里程计没有失效(例如,退化),并且估计的LiDAR角速度和线速度满足我们建议的评估标准(参见第III-C5节),则认为激励是足够的,并且LiDAR里程计输出和相应的IMU数据都被馈送到初始化模块(参见第III-C节)
在初始化中,首先通过移动IMU测量值来校准时间偏移,以与LiDAR里程计对准,然后进行优化处理,进一步细化时间偏移,校准外参,估计IMU偏差和重力矢量。通过融合后续的LiDAR和IMU数据,可以将初始化的状态附加到紧耦合的LiDAR惯性里程计(例如,[1]),用于在线状态估计。
激光里程计
我们的LiDAR里程计是建立在恒速(CV)运动模型上的,该模型假设在tk和tk+1接收到的两个连续扫描之间的角速度和线速度是恒定的,即,在tk和tk+1接收到的两个连续扫描之间,有:
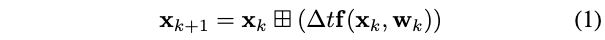
其中\(\Delta t\)是两帧扫描的时间间隔,状态向量\(\mathbf{x}\)、噪声\(\mathbf{w}\)和离散的状态转移函数\(\mathbf{f}\)定义如下:
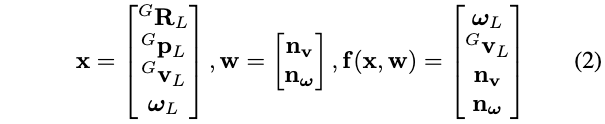
其中:
- \({ }^{G} \mathbf{R}_{L} \in S O(3)\)和\({ }^{G} \mathbf{p}_{L}\)分别表示激光雷达在全局坐标系(此处为第0帧激光坐标系)的姿态的位置
- \({ }^{G} \mathbf{v}_{L}\)是激光雷达在全局坐标系的速度表示
- \(\omega_{L}\)是激光雷达线速度(在激光雷达坐标系)
- 上述两个速度被分别被建模为由高斯噪声\(\mathbf{n}_{\mathbf{v}}\)和\(\mathbf{n}_{\omega}\)驱动的随机游走过程。
在对于公式(1),使用文献[22]的记号\(\boxplus / \boxminus\)紧凑地表示状态流形上的“+”。具体地说,对于公式(2)中的状态流形\(S O(3) \times \mathbb{R}^{n}\),运算及其逆定义如下:
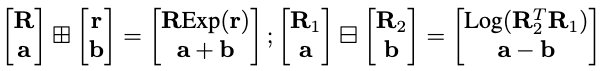
其中:
- \(\mathbf{R}, \mathbf{R}_{1}, \mathbf{R}_{2} \in S O(3)\),
- \(\mathbf{r}, \mathbf{a}, \mathbf{b} \in \mathbb{R}^{n}\)
- \(\operatorname{Exp}(\cdot): \mathbb{R}^{3} \mapsto S O(3)\) 表示指数映射
- \(\log (\cdot): S O(3) \mapsto \mathbb{R}^{3}\)是指数映射的逆,即对数映射
在实践中,传感器的运动可能不具有恒定速度。为了减轻这种模型误差的影响,我们可以将输入的LiDAR扫描分割成多个持续时间较短的子帧,在这些子帧上传感器的运动更符合CV模型。
误差迭代卡尔曼
基于流形上的系统表示(1),我们使用误差状态迭代卡尔曼过滤(ESIKF)[23]来估计其状态,ESIKF的预测步骤由状态预测和协方差传播组成,如下所示:
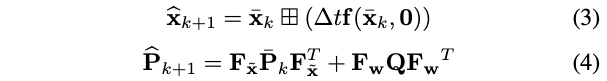
其中,
- \(\mathbf{P}\)表示状态估计的协方差
- \(\mathbf{Q}\)表示过程噪声\(\mathbf{w}\)对应的协方差
\(\mathbf{F}_{\tilde{\mathbf{x}}}\) 和 \(\mathbf{F}_{\mathbf{w}}\)定义如下:
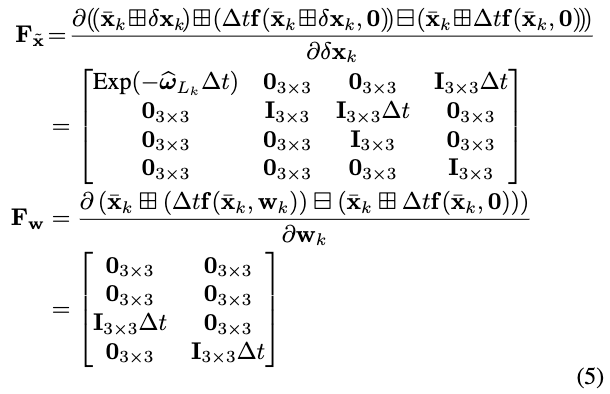
由误差状态微分方程可导出(上述Fx Fw是离散时间下的)
运动补偿
在我们考虑的问题中,IMU和LiDAR是不同步的,因此文献[14,15]所采用的IMU辅助运动补偿方法是不可行的。
在时间戳\(t_{k+1}\)处接收到新的激光雷达扫描之后,为了补偿运动失真,我们将在时间戳\(\rho_{j} \in\left(t_{k}, t_{k+1}\right)\)处采样的每个包含点\({ }^{L_{j}} \mathbf{p}_{j}\)投影到扫描端激光雷达帧\(L_{k+1}\)中,也就是将激光矫正到扫描结束时刻。
在恒速模型下,我们有\({}^G \widehat{\mathbf{v}}_{L_{k+1}}={}^G{\overline{\mathbf{v}}}_{L_{k}}, \widehat{\boldsymbol{\omega}}_{L_{k+1}}=\overline{\boldsymbol{\omega}}_{L_{k}}\),因此,可以导出\({}^{L_{k+1}} \check{\mathbf{T}}_{L_{j}}=\left({ }^{L_{k+1}} \check{\mathbf{R}}_{L_{j}},{ }^{L_{k+1}} \check{\mathbf{p}}_{L_{j}}\right)\)的计算如下:
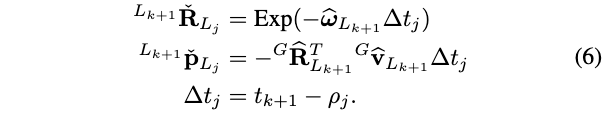
然后,在时间段\(\rho_{j} \in\left(t_{k}, t_{k+1}\right)\)内的测量\({ }^{L_{j}} \mathbf{p}_{j}\)可以被投影到扫描结束时刻,即:
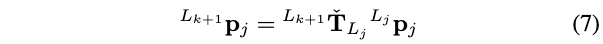
矫正之后的激光扫描\(\left\{ {}^{L_{k+1}} \mathbf{p}_{j}\right\}\)用于提供未知状态\({}^G \mathbf{T}_{L_{k+1}}\)的隐式测量,表示为点到面距离残差,在此基础上,在迭代卡尔曼滤波器框架中迭代估计完整状态\(\mathbf{x}_{k+1}\),直到收敛。这种迭代估计的细节可以参考FAST-LIO2[1]或[23],以便更一般地处理流形约束。
收敛后的状态估计记为\(\overline{\mathbf{x}}_{k+1}\),将用于传播后续IMU测量,如第III-B1节所述。
图3中示出了使用有运动补偿和无运动补偿的扫描的映射结果比较。

激光-惯性初始化
第III-B节中的激光雷达里程计在每个扫描结束时间\(t_{k}\)输出激光雷达的角速度\(\boldsymbol{\omega}_{L_{k}}\)和线速度\({ }^{G} \mathbf{V}_{L_{k}}\)。同时,惯性测量单元提供了原始测量,包括时间戳\(\tau_{i}\)的body系角速度\(\omega_{m}\)和线加速度\(\mathbf{a}_{m_{i}}\)。这些数据按照第III-C5节所示的激励标准进行累积和重复评估。
一旦收集到足够激励的数据,就调用初始化模块,然后输出如下信息:
- 时间偏移\({ }^{I} t_{L} \in \mathbb{R}\)
- 外参\({ }^{I} \mathbf{T}_{L}=\left({ }^{I} \mathbf{R}_{L},{ }^{I} \mathbf{p}_{L}\right) \in SE(3)\)
- IMU Bias\(\mathbf{b}_{\omega}, \mathbf{b}_{\mathbf{a}} \in \mathbb{R}^{3}\)
- 以及全局坐标系下的重力向量\({ }^{G} \mathbf{g} \in \mathbb{R}^{3}\)
- 数据处理
IMU原始测量数据收到噪声\(\mathbf{n}_{\omega_{i}}\) 和 \(\mathbf{n}_{\mathbf{a}}\)的影响,因此IMU测量模型如下:
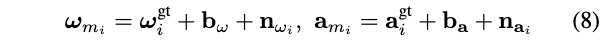
其中,
- \(\omega_{i}^{\mathrm{gt}}, \mathbf{a}_{i}^{\mathrm{gt}}\)是测量真值
- 同时,从激光里程计估计出来的\(\boldsymbol{\omega}_{L_{k}},{ }^{G} \mathbf{v}_{L_{k}}\)也包含了噪声
为了消除这些通常是高频的噪声,使用了非因果零阶低通滤波器[24]来过滤噪声,而不会引入任何过滤延迟。零相位过滤是通过巴特沃斯低通滤波器的前向和后向运行来实现的[24],得到噪声衰减(去除噪声影响的测量)的IMU测量\(\boldsymbol{\omega}_{I_{i}}=\boldsymbol{\omega}_{i}^{\mathrm{gt}}+\mathbf{b}_{\omega}, \mathbf{a}_{I_{i}}=\mathbf{a}_{i}^{\mathrm{gt}}+\mathbf{b}_{\mathbf{a}}\)为表示简单起见,噪声衰减的激光里程计速度估计值仍然表示为\(\boldsymbol{\omega}_{L_{k}},{ }^{G} \mathbf{v}_{L_{k}}\)。
从激光雷达里程计得到的\(\boldsymbol{\omega}_{L_{k}},^{G} \mathbf{v}_{L_{k}}\),通过非因果中心差分[25]得到激光雷达角加速度和线加速度\(\boldsymbol{\Omega}_{L_{k}},{ }^{G} \mathbf{a}_{L_{k}}\),因此,根据激光里程计得到的数据记为:
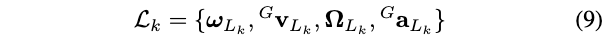
类似地,我们从噪声衰减的陀螺测量\(\omega_{I}\)得到角加速度\(\boldsymbol{\Omega}_{I_{i}}\),因此有:
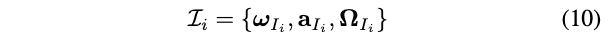
由于IMU频率通常高于LiDAR odometer的频率,因此两个序列\(\mathcal{I}_{i}\)和\(\mathcal{L}_{k}\)的长度并不相同。为了解决这一问题,我们提取在同一时间段内接收的LiDAR和IMU数据,并通过在每个LiDAR里程计时间\(t_{k}\)对\(\mathcal{I}_{i}\)进行线性插值来实现下采样(参见图4)。
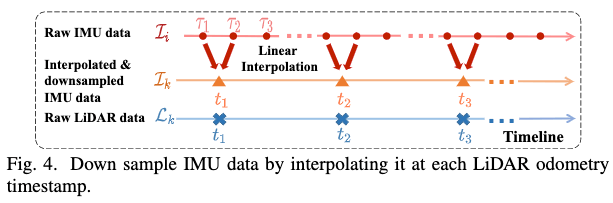
降采样的IMU数据记为\(\mathcal{I}_{k}\):
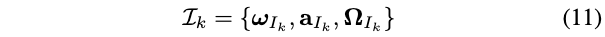
其中,\(\mathcal{I}_{k}\)具有与\(\mathcal{L}_{k}\)相同的时间戳\(t_{k}\)(但是数据实际上被已知的时间常数\({ }^{I} t_{L}\)延迟)。
- 用互相关法进行时间初始化(Temporal Initialization by Cross-Correlation)
在大多数情况下,由于LiDAR惯性里程计模块受到接收数据之前不可避免的传输和处理延迟,在LiDAR \(\mathcal{L}_{k}\)和IMU \(\mathcal{I}_{k}\)之间将存在未知但恒定的偏移\({ }^{I} t_{L}\)(例如IMU数据,全部向前推进\({ }^{I} t_{L}\),则与激光雷达数据对齐)。
由于激光雷达数据公式(9)和IMU数据公式(11)处于离散时间\(t_{k}\),因此IMU数据的推进实质上是以离散时间步\(d={ }^{I} t_{L} / \Delta t\)进行的,其中\(\Delta t\)是两次激光雷达扫描之间的时间间隔。具体地说,对于角速度,我们有:

忽略通常很小的陀螺偏置bω,我们发现\(\boldsymbol{\omega}_{I_{k+d}}\)和\(\boldsymbol{\omega}_{L_{k}}\)的大小(模长)应该是相同的,而与外参\({ }^{I} \mathbf{R}_{L}\)无关。受[16]的启发,我们使用互相关来量化它们之间的相似度。然后,偏移量\(d\)可以从下面的优化问题中求解:
 通过枚举\(\mathcal{L}_{k}\)的索引范围内的偏移量\(d\)。
通过枚举\(\mathcal{L}_{k}\)的索引范围内的偏移量\(d\)。
这里是通过对IMU数据逐个前挪来实现对齐,所以\(d\)的理解是:IMU前移1个数据,即前移了\(\Delta t\)时间,所以\({ }^{I} t_{L}= d * \Delta t\)
- 统一的旋转外参和时间校准
(2)中的互相关法对噪声和小尺度陀螺偏差具有较强的鲁棒性。但其的一个明显缺陷是,时间偏移的校准分辨率只能达到激光雷达里程计的一个采样间隔\(\Delta t\),不能识别任何小于\(\Delta t\)的剩余偏移δt。
设\({ }^{I} t_{L}\)为激光雷达里程计ωL与IMU数据ωi之间的总偏移量,则\({ }^{I_{t}} t_{L}=d^{*} \Delta t+\delta t\)。与公式(12)类似,如果IMU测量\(\boldsymbol{\omega}_{I}\)提前时间\({ }^{I} t_{L}\),则通过下式将与激光雷达里程计\(\omega_{L}\)对齐:
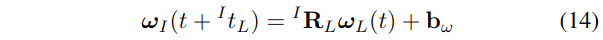
由于公式(9)中的实际激光雷达里程计\(\boldsymbol{\omega}_{L}\)仅在时间戳\(t_{k}\)处可用,用\(t=t_{k}\)和\({ }^{I} t_{L}=d^{*} \Delta t+\delta t\)代入到公式(14),并注意到\(\boldsymbol{\omega}_{L}\left(t_{k}\right)=\boldsymbol{\omega}_{L_{k}}\),我们有:
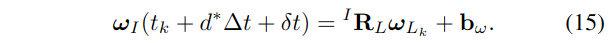
注意到,\(\boldsymbol{\omega}_{I}\left(t_{k}+d^{*} \Delta t+\delta t\right)\)是在时间戳为\(t_{k}+d^{*} \Delta t\)之后紧跟的IMU角速度,而时间戳为\(t_{k}+d^{*} \Delta t\)对应的角速度和角加速度分别为\(\omega_{I}\left(t_{k}+d^{*} \Delta t\right)=\omega_{I_{k^{\prime}}}\)和\(\boldsymbol{\Omega}_{I}\left(t_{k}+d^{*} \Delta t\right)=\boldsymbol{\Omega}_{I_{k^{\prime}}}\),假设角加速度在小量\(\delta t\)上恒定,我们可以插值得到\(\boldsymbol{\omega}_{I}\left(t_{k}+d^{*} \Delta t+\delta t\right)\):

将上式(16)代入公式(16),可以获得:
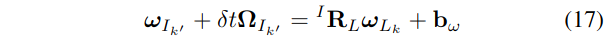
最后,基于公式(17)中的约束,统一的时空优化问题可以表述为:
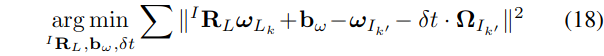
上述问题可通过Ceres迭代求解(由于非线性约束\({ }^{I} \mathbf{R}_{L} \in S O(3)\)),并且给定初始值为\(\left({ }^{I} \mathbf{R}_{L}, \mathbf{b}_{\omega}, \delta t\right)=\left(\mathbf{I}_{3 \times 3}, \mathbf{0}_{3 \times 1}, 0\right)\)
- 平移外参与重力向量初始化
在第III-C3节中,我们得到了外旋转\({ }^{I} \mathbf{R}_{L}\)、陀螺偏置\(\mathbf{b}_{\omega}\)和时间偏移量\({ }^{I} t_{L}\)。在这一部分中,我们将固定这些值,然后进行平移外参、重力矢量和加速度偏差的校准。
首先,我们使用之前得到的偏移\(d^{*}\)和\(\delta t\)来对齐IMU数据\(\mathcal{I}_{k}\)和雷达数据\(\mathcal{L}_{k}\)。对齐的IMU数据表示为̄\(\overline{\mathcal{I}}_{k}\),现在认为它与\(\mathcal{L}_{k}\)完全对齐,没有时间偏移。
具体地,在时间\(t_{k}\)对应于LiDAR角速度̄\(\boldsymbol{\omega}_{L_{k}}\)的IMU角速度\(\bar{\omega}_{I_{k}}\)为(其实就是公式(15)):
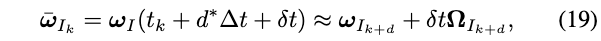
相似的,与时刻\(t_{k}\)的LiDAR加速度\({ }^{G} \mathbf{a}_{L_{k}}\)对应的IMU加速度̄\(\overline{\mathbf{a}}_{I_{k}}\)为:
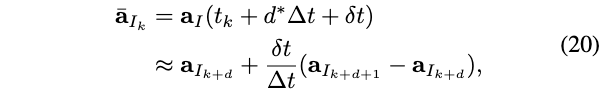
与公式(14)类似,我们可以找到IMU和LiDAR之间的加速度约束。如文献[26]所述,具有固定外参的两个坐标系A、B的加速度具有以下关系:
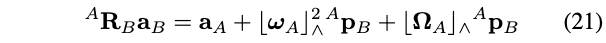
其中,
- \({ }^{A} \mathbf{R}_{B},{ }^{A} \mathbf{p}_{B}\)表示从B系到A系的外参变换
- \(\mathbf{a}_{A}, \mathbf{a}_{B}\)分别是加速度在两个坐标系的表示
上面公式(21)怎么来的,为啥不是 \({ }^{A} \mathbf{R}_{B} \mathbf{a}_{B}=\mathbf{a}_{A}\)
对于LiDAR-惯性系统,我们有两种选择:A用于IMU,B用于LiDAR,或者相反的情况。值得注意的是,在第一种情况下,\(\boldsymbol{\omega}_{A}=\overline{\boldsymbol{\omega}}_{I_{k}}-\mathbf{b}_{\omega}\)的精度受到陀螺仪偏差估计的影响,并且\(\boldsymbol{\Omega}_{A}\)的误差会因角速度测量中的噪声而被放大。
为了避免这一问题,增加外源平移校准的鲁棒性,我们将LiDAR设置为A,将IMU设置为B,由于LiDAR的加速度\({ }^{G} \mathbf{a}_{L_{k}}\)是在全局坐标系中(即第0帧激光坐标系)描述的,所以我们需要将这个加速度转换到激光雷达坐标系下,记为\(\mathbf{a}_{L_{k}}\):
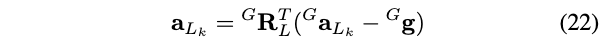
其中,\({ }^{G} \mathbf{R}_{L}\)是LiDAR在激光里程计全局坐标系的姿态,由第III-B节中的LiDAR里程计获得。
最后,平移外参、加速度计偏置和重力矢量可以从以下优化问题中联合估计:
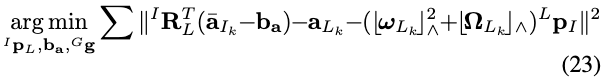
上述问题可以由ceres求解器迭代求解(由于约束\({ }^{G} \mathbf{g} \in \mathrm{S}_{2}\)),并且指定初始值\(\left({ }^{I} \mathbf{p}_{L}, \mathbf{b}_{\mathbf{a}},{ }^{G} \mathbf{g}\right)= \left(\mathbf{0}_{3 \times 1}, \mathbf{0}_{3 \times 1}, 9.81 \mathbf{e}_{3}\right)\)。
在估计\({ }^{L} \mathbf{p}_{I}\)之后,从激光雷达到IMU的转换计算如下:\({ }^{I} \mathbf{p}_{L}=-{ }^{I} \mathbf{R}_{L}^{L} \mathbf{p}_{I}\)
- 数据累积评估
提出的初始化方法依赖于LiDAR惯性器件的充分激励(充分运动)。因此,系统应该能够自行评估激励是否足以执行初始化。
理想情况下,可以通过公式(18)关于\(\left({ }^{I} \mathbf{R}_{L}, \mathbf{b}_{\omega}, \delta t\right)\)和公式(23)关于\(\left({ }^{I} \mathbf{p}_{L}, \mathbf{b}_{\mathbf{a}},{ }^{G} \mathbf{g}\right)\)的的全雅可比矩阵的秩来评估激励。
在实际中,我们发现,使用关于外参\({ }^{I} \mathbf{R}_{L}\)和\({ }^{I} \mathbf{p}_{L}\)的雅可比来评估运动就足够了,因为对外参的激发通常需要复杂的运动,这也会激发其他状态。因此,记\(\mathbf{J}_{r}\)为公式(18)对旋转外参\({ }^{I} \mathbf{R}_{L}\)的雅可比,\(\mathbf{J}_{t}\)为公式(23)对平移外参\({ }^{I} \mathbf{p}_{L}\)的雅可比,如下:
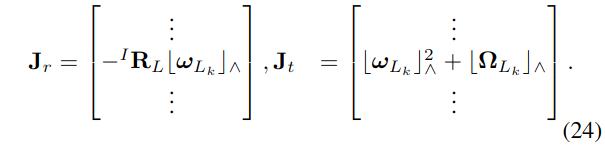
那么,激励可以通过对以下矩阵的秩来进行评估:
- \(\mathbf{J}_{r}^{T} \mathbf{J}_{r}=\sum\left\lfloor\boldsymbol{\omega}_{L_{k}}\right\rfloor{ }_{\wedge}^{T}\left\lfloor\boldsymbol{\omega}_{L_{k}}\right\rfloor \wedge\)
- \(\mathbf{J}_{t}^{T} \mathbf{J}_{t}=\sum\left(\left\lfloor\boldsymbol{\omega}_{L_{k}}\right\rfloor_{\wedge}^{2}+ \left\lfloor\boldsymbol{\Omega}_{\left.L_{k}\right\rfloor}\right\rfloor_{\wedge}\right)^{T}\left(\left\lfloor\boldsymbol{\omega}_{L_{k}}\right\rfloor_{\Lambda}^{2}+\left\lfloor\boldsymbol{\Omega}_{L_{k}}\right\rfloor \wedge\right)\)
更定量地,用\(\mathbf{J}_{r}^{T} \mathbf{J}_{r}\)和\(\mathbf{J}_{t}^{T} \mathbf{J}_{t}\)的奇异值来表示激发的程度。根据这一原理,我们开发了一个评估程序,可以指导用户如何移动他们的设备以获得足够的激励。我们根据雅可比矩阵的奇异值来量化激励,并用来评估激励是否充分。