Large-Scale LiDAR Consistent Mapping using Hierarchical LiDAR Bundle Adjustment

摘要
重建精确一致的大规模激光雷达点云图对机器人应用至关重要。现有的位姿图优化方法虽然效率高,但不能直接优化建图一致性。激光雷达束调整(BA)最近被提出来解决这个问题;然而,这在大尺度地图上太耗时了。为了解决这一问题,本文提出了一种适用于大尺度地图的全局一致且高效的制图方法。
我们提出的工作包括自底向上的层次BA和自顶向下的姿态图优化,结合了两种方法的优点。通过分层设计,我们用比原始BA小得多的Hessian矩阵大小解决了多个BA问题;通过姿态图优化,实现了激光雷达姿态的平稳高效更新。
我们提出的方法的有效性和鲁棒性已在多个空间和及时的大规模公共旋转LiDAR数据集上得到验证,如KITTI、MulRan和Newer College,以及结构化和非结构化场景下自收集的固态LiDAR数据集。通过适当的设置,我们证明了我们的工作可以在大约12%的序列时间内生成全局一致的建图。
介绍
激光雷达束调整(LiDAR bundle adjustment, BA)方法[5,6]通过最小化总体点面距离直接优化了建图一致性,这通常会带来高的建图质量,这是建图应用所必需的。在5中,首先解析求解平面参数,这样最终的优化问题只与LiDAR姿态有关。在6中,与visual BA[7,8]一样,通过Schur补技巧在每次优化迭代中消除平面参数。无论哪种方式,得到的优化结果(至少)是LiDAR位姿数N的维数,需要O(n3)时间来求解9。由于计算时间的三次增长,对于具有较大位姿数的大比例尺地图,无法进行束调整。
针对上述问题,我们提出了一种分层LiDAR BA方法,在保持时间效率的前提下全局优化建图一致性。该方法构建框架位姿的金字塔结构(如图1),并进行自底向上的层次BA调整和自顶向下的位姿图优化(如图2)。自底向上过程在从底层(局部BA)到顶层帧(全局BA)的局部窗口内进行层次BA调整。这样的设计大大提高了计算时间,每层局部BA的处理适合并行处理,而且由于涉及的位姿较少,每个局部BA的时间复杂度相对较低。自底向上过程中的一个问题是它忽略了在不同的局部窗口中共同可见的特征,这可能会降低精度。为了缓解这个问题,自顶向下的过程构造一个从上到下的位姿图,并通过位姿图优化分配错误。这两个过程迭代直到收敛。


通过分层BA调整设计,既可以直接优化点云内平面的一致性,又可以避免求解大维的代价函数。通过位姿图优化,我们以快速可靠的方式对整个激光雷达位姿进行适当的收敛更新。为了保持每两个相邻关键帧之间的平滑性,我们通过设置步幅大小小于窗口大小来保持它们之间的重叠区域。为了进一步提高优化速度,我们在构建金字塔时使用了滤波器去除异常点,并实现了基于cpu的并行处理。综上所述,我们的贡献如下:
- 提出了一种分层束调整方法,以全局优化激光雷达建图一致性和里程测量精度。在给定良好的初始位姿轨迹(例如,从位姿图优化)的情况下,我们提出的方法提高了建图质量,甚至在初始位姿轨迹有较大漂移时缩小间隙
- 我们提出的工作的有效性已经在多个公共机械旋转激光雷达数据集和我们自己收集的固态激光雷达数据集上进行了结构化和非结构化场景的验证
相关工作
文献中讨论了多种提高建图质量的方法,主要分为两类:基于位姿图优化的方法和基于平面(束)调整的方法。在位姿图优化中,两帧之间的相对变换(位姿约束)由ICP[10]或其变体估计[11,12]。这个相对位姿误差然后由信息矩阵加权,通常是对应的Hessian13的逆矩阵或简单的常数矩阵[14]。当总和相对位姿误差最小时,对位姿图进行优化。尽管姿态图优化的计算效率很高,但它的一个重要问题是不能直接优化点云的一致性。由于相对位姿约束的不正确估计或不精确建模,位姿图可能收敛到局部最小值,点云内仍可能存在较大的发散3,15。
平面调整方法通过最小化点到平面的总和距离,直接优化点云的一致性。在平面调整中,每个平面特征用两个参数表示,即平面到原点的距离和平面法向量6,在[16]中,作者同时优化了激光雷达姿态和几何平面特征。该方法在优化过程中需要对所有特征的参数进行维护和更新,而随着地图规模的扩大,特征的总数会迅速增长,导致代价函数的维数很大。虽然使用舒尔补法可以将优化变量简化为激光雷达位姿,但在实际操作中,该方法在优化过程中容易产生位姿估计故障。
BA调整方法改进了平面调整技术,通过在优化前消除特征估计参数,使用一个封闭形式的解5,在5中,作者将点云分割为多个体素,每个体素包含一个平面特征。将原来的点到面最小化问题转化为每个体素中点协方差特征值的最小化问题。这种方法需要遍历每个特征内的每个点来推导Hessian矩阵,而Hessian矩阵的时间复杂度是点数的平方,计算量很大。该问题在后续工作9中得到解决,该工作将同一姿态观察到的特征的所有点进行了聚合,从根本上消除了时间复杂度对点数的依赖。
尽管如此,在上述所有的平面和束调整方法中,计算复杂度仍然是位姿数量的三次方,对于大比例尺地图来说并不实用。此外,当地图中的散度大于或接近最大体素大小时,这些方法可能具有较慢的收敛速度。
我们提出的分层束调整方法同时利用了BA和姿态图优化。我们使用BA直接最小化点到面距离和位姿图优化来平滑有效地更新激光雷达的位姿,以避免位姿估计中的故障。通过分层设计,我们可以用比原来的5小得多的Hessian矩阵大小并行解决多个BA问题。此外,我们可以根据初始姿态轨迹的质量灵活地设置从底层到顶层的BA参数。
方法
概览
所提方法的系统工作流程如图2所示。输入是来自每次激光雷达扫描的原始点或去畸变点云,以及它们在全局坐标系中相应姿态的初始估计,这可以从一般激光雷达里程计或同步运动和建图(SLAM)算法中获得。该方法由两个过程组成,自底向上(见第III-B节)和自顶向下(见第III-C节),迭代直到收敛。

在自底向上的过程中,对较小的局部窗口内的LiDAR帧进行局部BA,构建从第一层到第二层的关键帧(如图1)。这个过程是分层执行的,直到满足最优层数,并在顶层关键帧上执行全局BA。然后利用各优化层和相邻层之间的因子构建位姿图(如图1所示)。

如图1所示,first layer(在上文中的bottom layer)描述了初始LiDAR帧和姿态的集合。类似地,second layer表示使用局部BA从first layer创建的LiDAR关键帧和姿态的集合。top layer是指最后剩下的LiDAR关键帧的集合(在图1中,顶层指第三层)。
核心思想:
- 从底层到顶层分层创建LiDAR关键帧的过程称为自底向上过程。
- 通过姿态图优化来更新底层激光雷达姿态的过程称为自顶向下过程。
自底向上的BA (Bottom-Up Hierarchical BA)
- 记\(\mathbb{F}_j^i\)为第i层的第j帧雷达,以及\(\mathbf{x}_j^i \triangleq \mathbf{T}_j^i=(\mathbf{R}, \mathbf{t}) \in \operatorname{SE}(3)\)为对应的位姿。
- 记\(\mathbf{T}_{j, k}^i\)为\(\mathbf{T}_j^i\)和\(\mathbf{T}_k^i\)的相对位姿,即\(\mathbf{T}_{j, k}^i=\left(\mathbf{T}_j^i\right)^{-1} \cdot \mathbf{T}_k^i\)
- 需要注意的是,\(\mathbb{F}_j^i\)是在雷达坐标系的点云,而位姿T是全局坐标系下的
- 此外,记\(w\)为局部窗口大小,\(S\)为自底向上构造LiDAR关键帧时的步幅大小,如图1所示。
假设我们有\(N_i\)帧点云(在第i层),在自底向上的过程中,利用所提供的初始姿态轨迹在每个局部窗口中进行局部BA,并优化每帧与该窗口第一帧之间的相对姿态。特别的,各局部窗口BA导出的Hessian矩阵H会被记录,并将其作为后续自顶向下的姿态图构造的信息矩阵。
给定一个在第i层,含有w帧点云的局部窗口\(\left\{\mathbb{F}_{s j+k}^i \mid j=0, \cdots,\left\lfloor\frac{N_i-w}{s}\right\rfloor ; k=0, \cdots, w-1\right\}\)及其优化之后的所有相对位姿\(\mathbf{T}_{j, k}^{i *}\),我们将这些帧聚合成第(i+1)层的一个关键帧。即每一帧中的所有点都转换到局部窗口的第一帧,新的关键帧的位姿\(\mathbf{T}_j^{i+1}\),其初值被设置为前一次局部窗口优化后的第一帧的pose。即有:
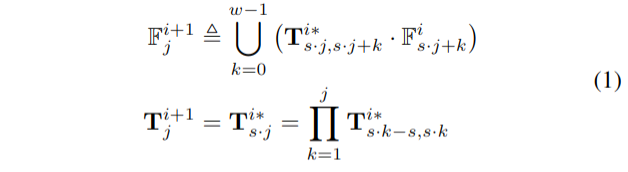
这一过程可以从下层到上层重复进行,直到达到最优层数\(l\)。值得注意的是,新的关键帧(局部BA)的构造不依赖于局部窗口外的帧,这使得可以同一层中的多个局部窗口并行处理。假设我们总共有N帧雷达点云,如\(N_1=N\),在每个时间,我们选择\(w\)帧以\(s\)为步长从低层到高层,设n为可用于并行处理的线程数。由于BA的计算时间为\(O\left(M^3\right)\), \(M\)为涉及的姿态数,我们可以推导出第\(l\)层金字塔的总时间消耗\(O\left(T_l\right)\)
第l层金字塔的总时间消耗包括每层局部BA消耗的时间和顶层全局BA消耗的时间。对于第l层金字塔,第i层的局部窗口数(i < l)为\(\frac{N}{s^i}\),每个局部窗口消耗\(O\left(w^3\right)\)个时间。当有n个并行线程时,本地BA的总时间消耗为各层本地BA的总和,即\(w^3 \cdot\left(\sum_{i=1}^{l-1} \frac{N}{s^i} \cdot \frac{1}{n}\right)\),以及第l层的全局BA花费时间为:\(O\left(\left(\frac{N}{s^{l-1}}\right)^3\right)\)。因此,第l层的时间复杂度总结如下:
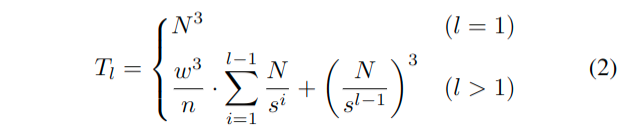
我们把\(T_l\)看作l的函数,通过让\(T_l\)的导数等于零来计算最优\(l^*\),这就得到:

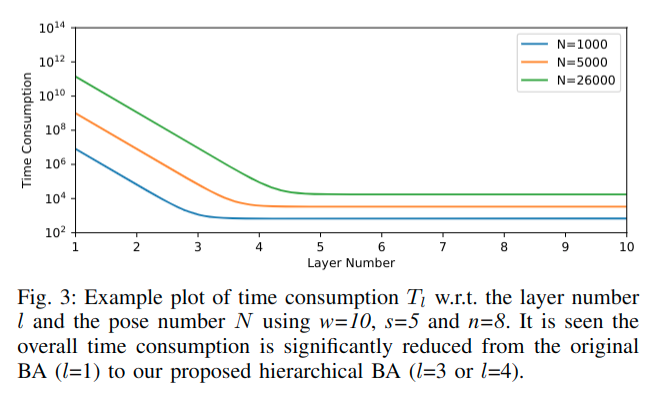
图3给出了不同帧数N时,计算时间\(T_l\)随层数l的变化示例,可以看出,随着层数从l=1(原始BA)增加到\(l^*\),计算时间大大减少,这表明了所提出的分层BA的有效性。当\(l > l^*\)时,计算时间不会增加太多,几乎保持不变,这表明任何大于\(l^*\)的层数都同样有效。
对于自底向上的分层BA中各层的特征提取和关联,我们使用5(BALM)中提出的自适应体素化方法,提取适合不同结构环境的不同大小的平面特征。为了提取这些不同尺寸的平面特征,整个点云在使用初始姿态轨迹转换为相同的全局坐标系后,被分割成大小为V的多个体素,每一个都通过平面测试,检查所含点的最小(V1)和最大特征值(V3)之比小于阈值,如\(\frac{\lambda_1}{\lambda_3}<\theta\),如果平面测试通过,体素中的点将被视为位于同一平面上并在BA中使用,否则,体素将被递归分割,直到包含的点形成一个平面。
上述自适应体素化过程在点数非常大的情况下非常耗时。为了缓解这个问题,我们注意到在低层中不被认为是平面特征的点在上层中也不会形成平面。因此,在自底向上的过程中,我们只使用局部BA中每个体素的平面特征点来构造上层的关键帧。该方法进一步节省了下一层自适应体素图构建的时间,提高了局部BA的计算精度。