Fundamentals of Inertial Navigation, Satellite-based Positioning and their Integration

目录
章节介绍
第二章
描述导航的数学、导航中使用的坐标框架以及在适当的坐标中计算导航解决方案所使用的转换。
第三章
讨论了GPS,详细介绍了GPS的各个部分、信号结构以及从伪距离和距离测量中估计位置和速度的过程。本文还讨论了在处理GPS数据时可能出现的各种误差。最后详细介绍了如何从星历表数据计算卫星的位置和速度,包括单频GPS接收机的大气校正。
第四章
介绍了惯性传感器及其分类、误差、标定、初始化和对准过程,然后描述了惯导系统机械化过程及其方程。
第五章
给出了一些基本的运动数学,并详细描述了在各种参考系下的机械化过程,给出了在最常见的导航系中导航参数的一步一步计算。
第六章
对惯导系统误差进行建模,并对惯导系统方程进行线性化。
第七章
讨论了KF的过程和测量模型、滤波算法、非线性滤波技术以及如何对系统扰动建模。
第八章
将所有这些想法与INS/GPS集成的详细描述以及相关的细微差别和微妙之处结合在一起。它描述了集成的类型以及它们的反馈方案。推导了INS动态误差模型方程和惯性传感器误差模型方程,讨论了线性化KF在松耦合和紧耦合INS/GPS融合中的实现。
第九章
讨论了轮式车辆的一种可能趋势,即通过使用速度读数来减少低成本惯性传感器的数量,并介绍了不同的约束以消除与6轴imu相关的误差,并实现类似的精度
第十章
给出了INS/GPS融合的实验结果。基于真实道路测试轨迹,分析了集成完整IMU(包含所有6个传感器)和简化系统(包含更少传感器)的结果。
第一章
1.6 INS/GPS组合类型
已经提出了不同形式的INS/GPS集成体系结构,以获得最大优势,这取决于使用类型和简单程度与鲁棒性。三个主要的集成体系结构是
- 松耦合
- 紧耦合
- 超紧密的或深耦合
Loosely Coupled INS/GPS Integration
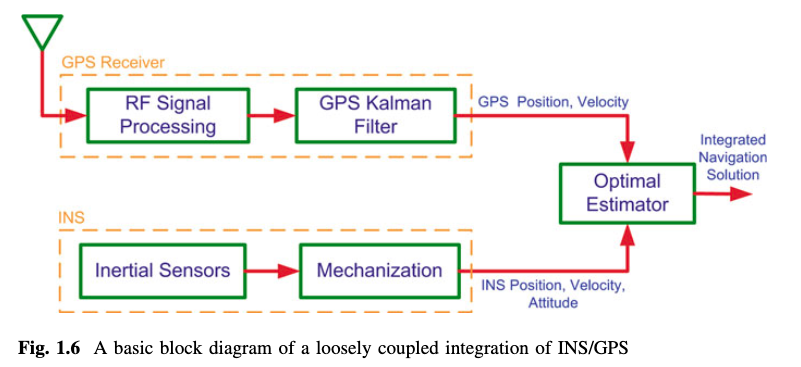
在这种架构中,也被称为松耦合,GPS和INS独立工作,并为位置、速度和姿态提供单独的解决方案。为了获得两个解的最佳解,这些信息通过最优估计器融合在一起,以获得第三个和大大改进的解。这种排列方式如图1.6所示。
Tightly Coupled INS/GPS Integration
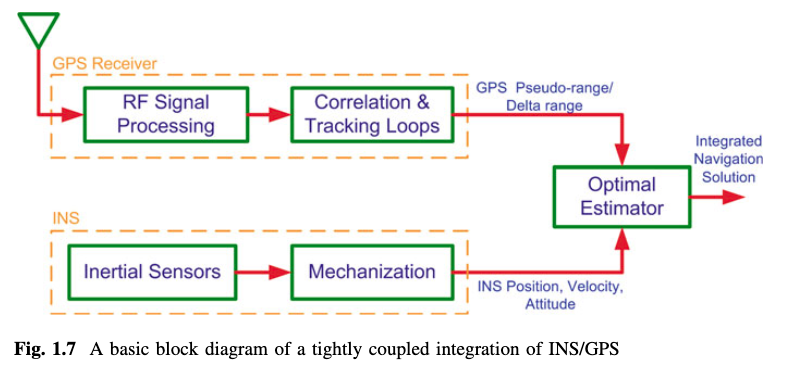
在这种架构中,也称为集中式集成,GPS和INS作为基本传感器,它们的伪距离和伪距离率的原始输出以及INS的加速度和旋转速率由单个估计器混合,以实现协同解决方案(Yang 2007)。这种排列如图1.7所示。
如第八章所述,GPS/INS集成可以通过多种方式实现,每种方式都有其优点和局限性
Ultra-Tightly or Deeply Coupled Integration
深度耦合集成增加了INS和GPS之间的共生关系,因为集成是在跟踪环级别。这样做的主要优点是利用多普勒信息在GPS跟踪回路中对host vehicle的动态进行估计和补偿。超紧密集成存在多种构型,图1.8为一种基本构型。估计器将来自GPS的伪距离/多普勒或I(同相)和Q(正交)测量值与INS导航参数结合起来,以呈现估计的多普勒(Alban et al. 2003)。估计的多普勒是用来消除动态从GPS信号进入跟踪环,从而减少载波跟踪环带宽。虽然这种集成更加复杂,需要访问GPS硬件,但它可以提高原始测量的质量和信号的抗干扰性能(Cox Jr 1978)。
第九章
9.3.2 轮式陆地车辆三维RISS的优点
3D RISS相对于2D车辆航迹推算解决方案的优势是基于两个加速度计的测量结果用于计算离面运动。主要体现为3个方面:
(1)第一个好处是计算正确的方位角。这是因为陀螺仪安装在车身并非严格水平,因此测量值并非完全是E-N平面的角速率。由于方位角在E-N平面,检测和修正陀螺仪倾斜的做法比忽略这一影响的二维车辆航迹推算更准确地计算出方位角。
(2)第二个好处是2D水平定位比2DRISS更精确,原因有二:
- 从里程表测量的速度计算两个水平速度时考虑了俯仰角,提供更准确的速度来实现更好的位置估计
- 更精确的方位角计算可以更好地估计东向与北向速度
(3)第三个好处是可以计算上升速度和高度,这是以前无法获得的数据
与完整的IMU相比,所提出的3D RISS的优点是通过加速度计而不是陀螺仪计算俯仰和横滚,并且通过里程表衍生的速度而不是加速度计计算车辆的速度。
为了证明从加速度计而不是陀螺仪来计算俯仰和横滚的优越性,假设陀螺仪中存在一个未补偿的bias,这将在俯仰或横滚中引入与积分产生的时间成正比的角度误差,从而导致INS的misalignment,从而将加速度矢量从机体框架错误地投影到局部框架。进一步的,在局部坐标系的一个水平通道中引入加速度误差,这将产生与\(t^2\)成正比的速度误差和与\(t^3\)成正比的位置误差。
当从加速度计计算俯仰和横摇时,第一次积分被消除,角度的误差与时间不成比例。此外,由这些角度误差引起的位置误差的部分将与\(t^2\)成比例,而不是\(t^3\)。
除了使用两个加速度计而不是两个陀螺仪来计算俯仰和横滚的优点之外,RISS还进一步改进了速度计算,使用里程表而不是加速度计计算速度(根据施加在陆地车辆上的非完整约束)比使用加速度计计算速度获得更好的性能。这是因为当从加速度计计算速度时,任何未补偿的bias都会在速度上引入与t成正比的误差,在位置上引入与\(t^2\)成正比的误差。从里程表计算速度避免了第一次积分,从而使位置计算只需要一次积分。这意味着当使用里程表测量时,位置是在一次积分后获得的,而不是使用加速度计测量连续两次积分。在长时间的GPS停机中,使用加速度计计算的位置误差将与停机持续时间的平方成正比。
作为上述两项改进的结果,位置计算的进一步改进将随之而来。使用加速度计计算的roll和pitch误差将导致惯导系统产生misalignment,从而影响速度从body系投影到局部坐标系,使由俯仰和横滚误差引起的位置误差部分与t成正比,而不是与\(t^2\)成正比,这是在消除两个陀螺仪的第一个改进中讨论的。
3D RISS中唯一剩下的主要误差来源是由于方位角陀螺仪造成的方位角误差。这个陀螺仪的未补偿的bias将导致方位角误差与时间成正比。由于这个方位误差而产生的位置误差将与车辆的(速度、积分时间和方位误差)成正比。这必须在积分滤波器内部通过模拟陀螺仪的随机漂移来解决。
此处有一部分轨迹杜比
9.3.3 三维RISS运动方程的推导
本节将介绍三维RISS的非线性运动模型,包括位置、速度和姿态状态
使用通用参考系。所述车辆车身框架的x轴沿横向方向,y轴沿向前纵向方向,z轴沿车辆垂直方向。局部框架是ENU框架,轴沿东、北和垂直(向上)方向。在k-1时刻从车体坐标系变换到局部坐标系的旋转矩阵为:
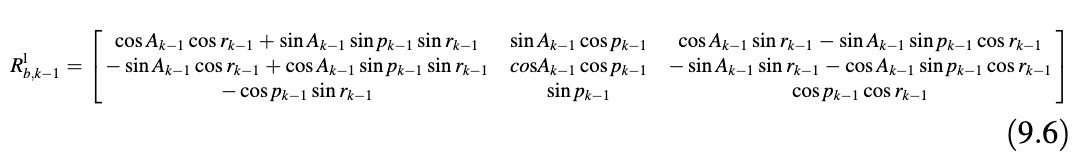
为了描述运动模型,我们首先需要控制输入。陀螺仪、两个加速度计和里程表提供的传感器测量表示为矢量:
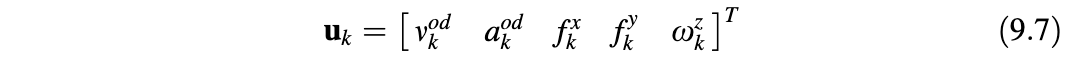
其中,
- \(v_k^{o d}\)表示轮式里程计计算得到的速度
- \(a_k^{o d}\)表示轮式里程计推导计算得到的加速度
- \(f_k^x\)表示横向加速度计的测量
- \(f_k^y\)表示前向加速度计的测量
- \(\omega_k^z\)表示方位角陀螺仪测量得到的角速度
- 在本讨论中,带有k后缀的控制输入表示那些导致系统状态在时间epoch k-1到k之间发生变化的输入
在推导运动方程之前,定义系统的导航状态是很重要的。一个可能的状态向量是:
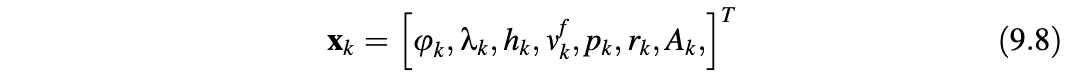
其中,
- \(\varphi_k\)是纬度
- \(\lambda_k\)经度
- \(h_k\)高度
- \(v_k^f\)前向速度
- \(p_k\)pintch角
- \(r_k\)roll角
- \(A_k\)方位角
pitch和roll的计算
对于陆地车辆,俯仰角是它相对于水平地面所作的角度(即围绕横向轴旋转),滚转角是其围绕纵向轴旋转,如图9.5所示。
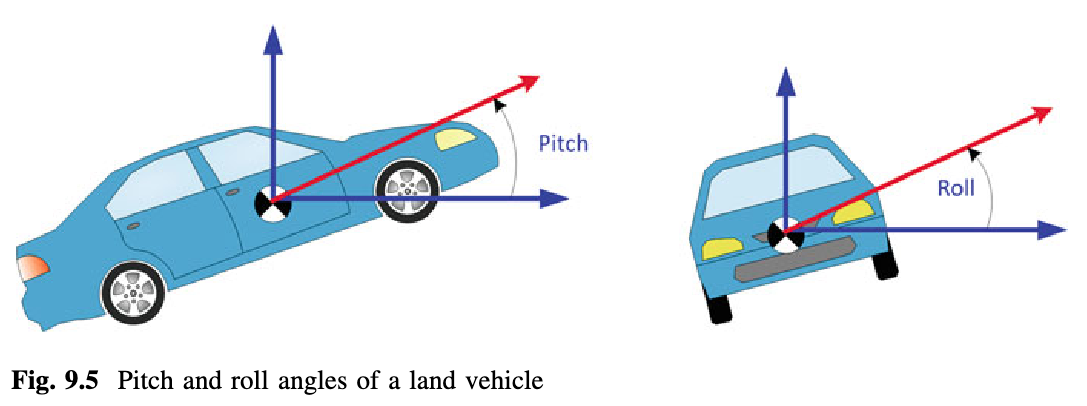
当车辆移动时,向前加速度计测量向前车辆加速度以及重力分量,并且为了计算俯仰角,从里程表测量中得到的车辆加速度,并且从向前加速度计测量中去除,如下:
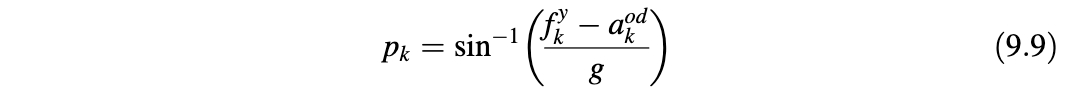
类似地,横向加速度计测量车辆加速度的法向分量以及重力分量,为了计算滚转角度,横向加速度计的测量必须补偿加速度的法向分量,也就是说,考虑车发生俯仰角的时候,重力分量不完全是g,而是\(g \cos p_k\):