An analytic solution to Wahba's problem

摘要
所有航天器姿态估计方法都是基于Wahba优化问题。这个问题可以简化为寻找Davenport矩阵的最大特征值和相应的特征向量。为了降低计算量,提出了QUEST和FOMA等迭代算法。但由于迭代次数不固定,求解结果理论上不准确,计算时间难以预测。最近,有人提出了一种解析解——ESOQ。解析解的优点是计算时间是固定的,在没有数值误差的情况下,理论上解是准确的。在本文中,我们对Wahba问题提出了一种不同的解析解。我们用简单且易于验证的例子表明,该方法在数值上比ESOQ更稳定,比QUEST和FOMA更快。我们还使用了大量的模拟测试来支持这一说法
介绍
姿态确定是每一个航天器系统成功的关键环节[1]。航天器姿态确定与估计问题是Wahba[2]在1965年提出的一个优化问题。第一种解决方案由Davenport[6]提出。Davenport证明了Wahba的问题等价于寻找所谓k矩阵的最大特征值和对应的特征向量。由于当时的计算机和相关算法还不够强大,无法将Davenport的方法应用到MAGSAT航天器的实时姿态和控制系统中[3],因此设计了QUEST算法[3]来满足这一需求。此后,QUEST被广泛认可并应用于许多航天器姿态确定和控制系统中,同时还提出了一些其他方法,如ESOQ[4]和FOMA[5]。QUEST和FOMA使用牛顿迭代来寻找以不同方式表示的四次多项式的最大解。尽管QUEST方法的所有飞行经验都是成功的,但[8]表明,通过使用特定的例子,QUEST可能不会收敛。事实上,众所周知,牛顿的方法是不适合一般使用的,因为它可能不能收敛到一个解。即使它确实收敛,它的行为在函数非凸的区域可能是不稳定的[9]。此外,由于QUEST和FOMA的求解依赖于迭代,并且是数值求解,这意味着求解不精确,计算时间不可预测。
注意到4次多项式(四分次)允许解析解,Mortari设计了Wahba问题的闭式解[4],其中使用四次根的一组公式代替牛顿方法(四次多项式的根有几组不同的解析公式)。在本文中,我们提出了一个由Shmakov[11]最近发现的替代解析解。Mortari的ESOQ和提出的解决方案的主要区别在于,后者的辅助立方是凹陷形式,而前者的辅助立方不是。因此,基于Shmakov公式的方法更为有效。仿真实验表明,该方法在数值上比ESOQ更稳定,与QUEST相当。
Wahba优化问题描述及其解法
Wahba的问题
给定一组单位向量\(r_i\)(表示参照系中物体的观测值)和一组单位向量\(b_i\)(表示航天器体坐标系中的测量值),航天器的姿态由满足关系的正交矩阵\(A\)定义,即满足:
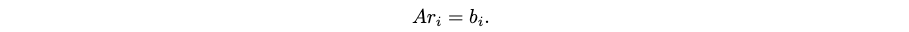
因此,姿态确定问题是寻找使Wahba损失函数最小的正交矩阵A:
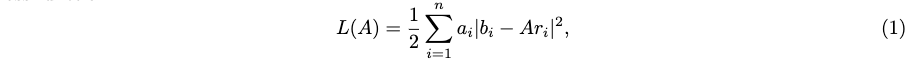
SVD解法
此处引用西北工业大学严恭敏老师的《捷联惯导算法与组合导航原理》第7章——初始对准与组合导航技术中的描述:

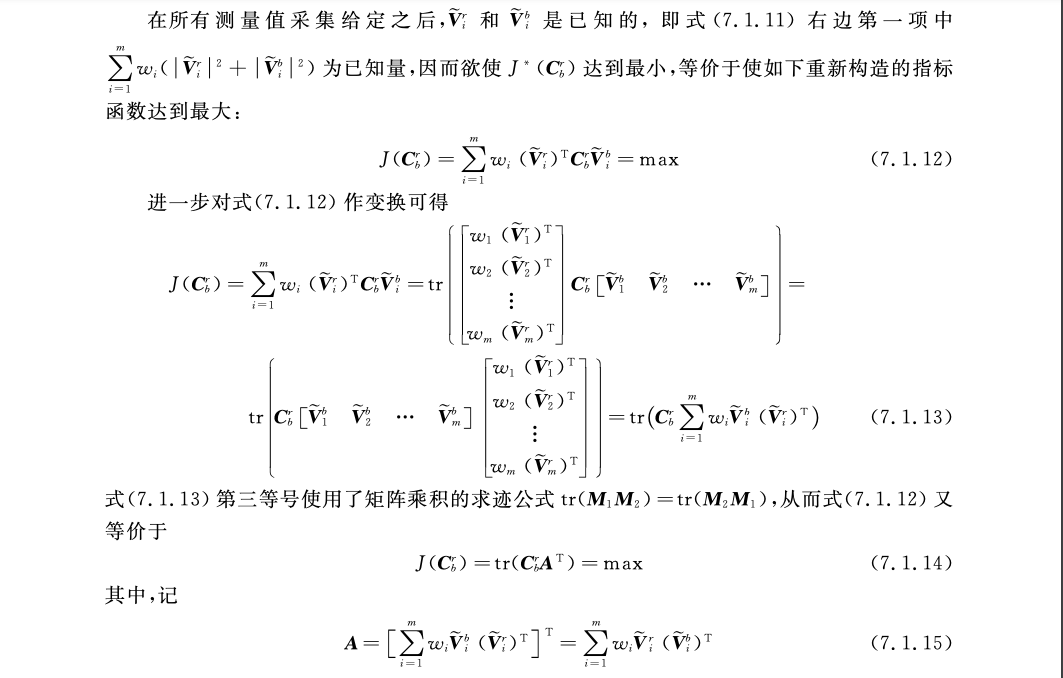

参考资料:
- 《捷联惯导算法与组合导航原理》第7章
- https://ahrs.readthedocs.io/en/latest/filters/davenport.html
四元数解法
也称Davenport’s q-Method
根据四元数与姿态阵的关系:
\[ \boldsymbol{C}=\left(q_0^2-\boldsymbol{q}_v^{\mathrm{T}} \boldsymbol{q}_v\right) \boldsymbol{I}+2 \boldsymbol{q}_v \boldsymbol{q}_v^{\mathrm{T}}+2 q_0\left(\boldsymbol{q}_v \times\right) \]
可以把上述“SVD解法”中的问题转换为关于四元数Q的目标函数:
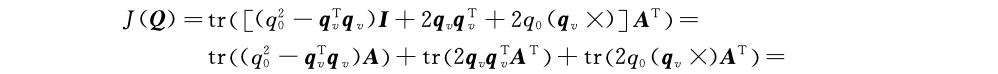

参考资料:
- 《捷联惯导算法与组合导航原理》附录k
- https://ahrs.readthedocs.io/en/latest/filters/davenport.html
- Paul B. Davenport. A Vector Approach to the Algebra of Rotations with Applications. NASA Technical Note D-4696. August 1968.