SR-LIO: LiDAR-Inertial Odometry with Sweep Reconstruction

摘要
此论文所述的BA不是对激光多帧的BA,而是多传感器融合的最小二乘。
基于改进的束平差(BA)框架,提出了一种新型激光雷达惯性里程计(LIO),命名为SR-LIO。SR-LIO的核心是一种新的扫描重建方法,该方法对旋转激光雷达的原始输入扫描进行分割和重建,以获得更高频率的重建扫描。该方法可以有效缩短每次IMU预积分的时间间隔,减小IMU预积分误差,实现基于BA的LIO优化。为了使重建扫描期间的所有状态都能均匀优化,我们进一步提出了多段联合LIO优化,该优化允许每个扫描段的状态同时受到LiDAR和IMU的约束。在三个公共数据集上的实验结果表明,我们的SR-LIO在精度上优于所有现有的最先进的方法,通过提出的扫描重建来减少IMU预积分误差对于基于BA的LIO框架的成功非常重要。
介绍
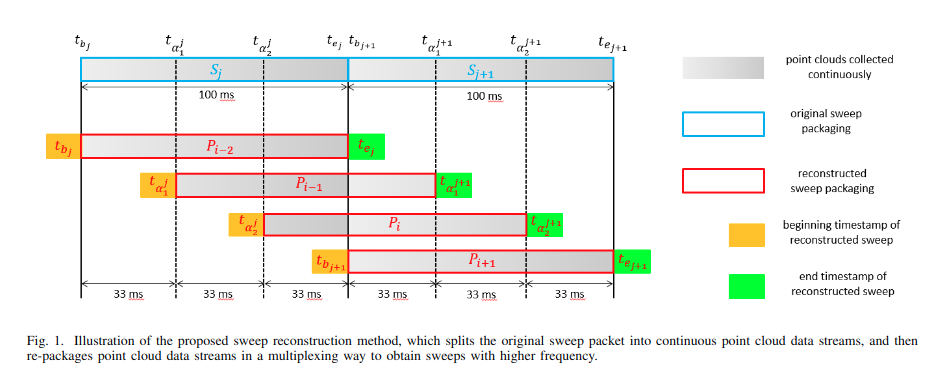
本文提出了一种扫描重建方法,即对自旋激光雷达的原始输入扫描进行分割和重建,以获得更高频率的重建扫描。具体而言,扫描重建方法利用旋转激光雷达连续扫描的特性,将每次全扫描分割为3个扫描段,然后将每个扫描段与接下来的2个扫描段依次连接,得到重构的全扫描(如图1所示)。对每个扫描段执行上述步骤后,每个原始扫描变成3个重构的全扫描,其频率提高3倍。增加的频率缩短了两次连续扫描之间的时间间隔,从而减少了IMU预集成的误差。因此,扫描重构不仅可以提高扫描频率,还可以通过减小IMU预积分误差来提高LIO联合优化的精度。
我们在前期的研究中发现,基于BA的框架对IMU预积分误差非常敏感。为了解决这个问题,我们将提出的扫描重建方法集成到基于ba的LIO系统中,从而得到SR-LIO。所提出的SR-LIO首先对10 Hz的输入扫频进行下采样,然后进行扫频重构以获得30 Hz的重构扫频。接下来,对于每一次重构扫描,我们执行LIO联合状态优化,其中IMU预积分周期为33ms,但重构后的扫描保持完整的扫描,持续时间为100ms(如图1所示)。为了更好地保持轨迹一致性,我们提出了一种新的多段联合优化方法,该方法充分利用IMU约束和位于每100ms周期的状态变量进行优化。优化当前重构扫描的状态后,将当前重构扫描的点云添加到地图中。由于在连续重建扫描中存在重复点,因此我们以与原始输入扫描相同的频率(10 Hz)执行地图更新,以防止重复添加相同的点云。
总结起来,本工作的主要贡献有三个方面:
- 提出了一种扫描重构方法,提高了LIO系统中激光雷达自旋扫描频率,降低了IMU预集成误差;
- 我们将所提出的扫描重建方法嵌入到新设计的基于BA的LIO系统中,实现了先进的扫描重建精度
- 开源
符号约定
坐标系统
我们记\((\cdot)^w,(\cdot)^l\) and \((\cdot)^o\)分别表示世界坐标系、激光雷达坐标系、IMU坐标系下的3D点。世界坐标在起始位置与\((\cdot)^o\)重合。
我们记在时间\(t_i\)执行激光扫描的激光坐标系为\(l_i\),那么其对应的IMU坐标为\(o_i\),那么(以外参而言)从\(l_i\)到\(o_i\)的转换矩阵记为\(\mathbf{T}_{l_i}^{o_i} \in S E(3)\):
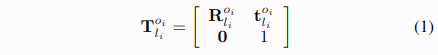
其中,\(\mathbf{T}_{l_i}^{o_i} \in S E(3)\)包含了一个旋转矩阵\(\mathbf{R}_{l_i}^{o_i} \in S O(3)\)和平移向量\(\mathbf{t}_{l_i}^{o_i} \in \mathbb{R}^3\)。
外参通常离线校准一次,并在在线姿态估计期间保持不变。因此,为了简单起见,我们可以使用\(\mathbf{T}_{l}^{o}\)表示\(\mathbf{T}_{l_i}^{o_i}\)
在下面的语句中,为了简化符号,我们省略了表示坐标系的索引。例如,从IMU坐标到世界坐标的姿态被严格定义为\(\mathbf{T}_{o_i}^w\),但为了简单起见表示为\(T^w_i\)
除了位姿,我们还估计了速度v、加速度计偏置ba和陀螺仪偏置bg,它们由状态向量均匀表示:
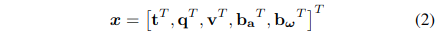
扫描状态表达
受CT-ICP[6]的启发,我们表示一个扫描的状态:
- (1)扫描起始时刻\(t_b\)的状态\(\left.S \text { (e.g., } \boldsymbol{x}_b\right)\)
- (2)扫描结束时刻\(t_e\)的状态\(S\) (e.g., \(\left.\boldsymbol{x}_e\right)\)
- 因此,在\(\left[t_b, t_e\right]\)时间区间内的点云,可以表示为关于\(\boldsymbol{x}_b\)和\(\boldsymbol{x}_e\)的函数,例如,在时间\(t_{\mathbf{p}} \in\left[t_b, t_e\right]\)采集点云,那么在此时间段内的状态可以表示为:
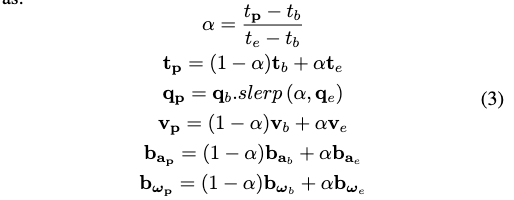
其中,\(\operatorname{slerp}(\cdot)\)表示四元数球面插值。
IMU测量模型
IMU由加速度计和陀螺仪组成。IMU的原始陀螺仪和加速度计测量值\(\hat{\mathbf{a}}_t\) and \(\hat{\boldsymbol{\omega}}_t\)表示如下:
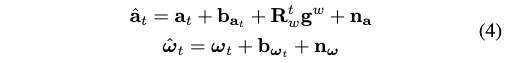
正如在Vins-Mono[20]中提到的,加速度和陀螺仪测量中的加性噪声可以建模为高斯白噪声,\(\mathbf{n}_{\mathrm{a}} \sim N\left(\mathbf{0}, \boldsymbol{\sigma}_{\mathrm{a}}^2\right), \mathbf{n}_{\boldsymbol{\omega}} \sim N\left(\mathbf{0}, \boldsymbol{\sigma}_{\boldsymbol{\omega}}^2\right)\)。加速度偏置和陀螺仪偏置建模为随机游走,其导数为高斯分布,\(\dot{\mathbf{b}}_{\mathrm{a}_t}=\mathbf{n}_{\mathbf{b}_{\mathrm{a}}} \sim N\left(\mathbf{0}, \sigma_{\mathbf{b}_{\mathrm{a}}}^2\right)\),\(\dot{\mathbf{b}}_{\omega_t}=\mathbf{n}_{\mathbf{b}_\omega} \sim N\left(\mathbf{0}, \sigma_{\mathbf{b}_\omega}^2\right)\)
扫描重组(论文核心)
扫描重组旨在从10Hz原始输入激光雷达扫描S中获得30Hz重组扫描P,图1说明了我们的核心思想

给定上一帧扫描\(S_j\)(扫描起始时刻:\(t_{b_j}\),扫描结束:\(t_{e_j}\))以及当前帧扫描扫描\(S_{j+1}(\)起始时刻:\(t_{b_{j+1}}\),扫描结束:\(t_{e_{j+1}}\)),我们假设时间段[\(t_{b_j}\), \(t_{e_j}\)]和[\(t_{b_{j+1}}\), \(t_{e_{j+1}}\)]的时长都是100ms。基于激光雷达在一段时间内连续采集的特点,我们可以将原始扫描数据包拆分为连续的点云数据流,然后对点云数据流进行复用重新打包,从而获得更高频率的扫描。