X-ICP: Localizability-Aware LiDAR Registration for Robust Localization in Extreme Environments
摘要
现代机器人系统需要在具有挑战性的环境中运行,这就要求在具有挑战性的条件下进行可靠的定位。基于激光雷达的定位方法,如迭代最近点(ICP)算法,在几何信息匮乏的环境中可能会受到影响,这些环境已知会降低配准性能,并将优化推向弱约束方向的发散
为了克服这个问题,本工作提出了 1)一个鲁棒的多类别(非)可定位性检测模块,以及 2)一个基于可定位性约束ICP优化模块,并以统一的方式将两者耦合在一起。所提出的可定位性检测是通过利用扫描和地图之间的对应关系来分析针对优化主方向的对准强度来实现的,作为LiDAR定位分析的一部分。
在第二部分中,这种可定位性分析紧密集成到扫描到地图的点云配准中,以沿着良好约束的方向生成无漂移的姿态更新。该方法经过了全面的评估,并在模拟和真实世界的实验中与最先进的方法进行了比较,从而在具有激光雷达挑战性的场景中获得了性能和可靠性的提升。在所有实验中,所提出的框架证明了准确和通用的定位检测和鲁棒的姿态估计,而不需要特定环境的参数调整。
介绍
点云配准局限性:
尽管ICP算法及其变体是迄今为止首选的注册方法之一,但在使用它时需要考虑其在实际应用中的局限性。[13],[14]发现有四种不同的误差来源会影响ICP算法。这些问题包括:
- 收敛到局部最小值的风险
- 对传感器偏差和噪声的敏感性
- 不准确的初始转换
- 以及在潜在的优化问题中缺乏几何约束
虽然机器人社区开发了减少前三个来源的方法和系统,但后者仍然可能导致现代机器人系统在困难环境中部署时发生故障。在(近)自对称环境中,沿对称轴的几何约束(几乎)与噪声构成的约束难以区分。因此,优化可能收敛到以噪声主导的最优解15,称为退化或退化情况。隧道、开放空间、走廊和门道都可能是这种退化环境的实例[16],参见图1中真实地下隧道示例的顶部一行。
考虑可定位性:
为了使机器人能够在所有场景中运行,包括退化的平面或类似隧道的环境,需要所谓的可定位性考量localizability-awareness[17]-[19]。
[17]: Learning-based Localizability Estimation for Robust LiDAR Localization (L3E)
应对机制是双重的:
- 首先,退化场景的检测
- 其次,减轻其对优化的负面影响
多种方法利用信息论将优化的退化检测为退化与否(二进制形式)——而不单独考虑运动的各个轴的退化情况20-23
然而,尽管具有实用性和简单,但这种分析并没有提供足够的细节,来说明优化过程中的退化方向。因此,大多数解决方案[18]-20更倾向于丢弃整个测量的配准结果,而不是至少沿着信息良好的方向对问题进行强化。
此外,如[17]描述,现有的检测方法如15、24在实践中表现良好,但需要对不同的环境或传感器配置进行繁琐的参数调整。
提出的方法:
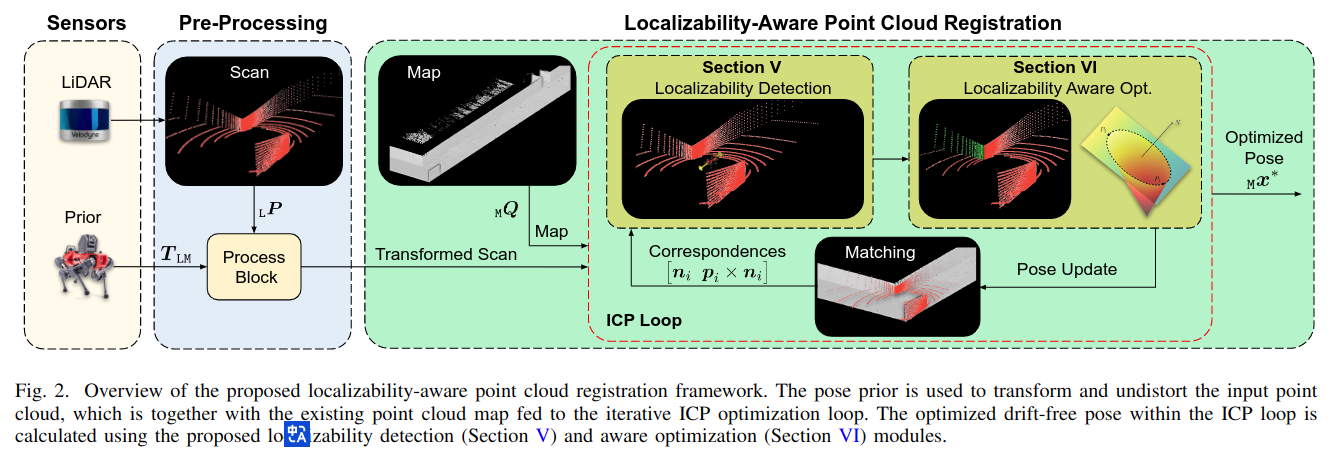
针对上述挑战,本文提出了一种鲁棒的可定位感知点云配准框架X-ICP,该框架使基于lidar的SLAM系统能够在无特征极端环境中运行。所提出的框架,如图 2 所示,解决了退化的检测和缓解。这两个子模块是可定位性检测模块,缩写为Loc.-Module,优化模块,缩写为Opt.-Module
Loc.-Module利用扫描与地图之间的点和表面法线对应关系来分析沿优化主方向的对齐强度。与之前的工作L3E[17]相比,这种可定位性检测用于scan-to-map,并且与机器人的朝向(相对于环境)无关。允许在各种环境配置中进行可靠的检测,例如地下场景,以及室外大场景,且无需在线参数调整。结果估计是细粒度的,即将当前机器人状态分为{可定位,部分可定位和不可定位}类别。
另一方面,Opt.-Module利用可定位性信息计算并整合优化约束,对点云配准进行底层优化,值得注意的是,Opt . module独立于ICP成本函数,可以与其他基于优化的系统单独结合使用。通过在迭代优化过程中直接考虑退化方向,减轻了退化方向的不利影响。这种优化的结果利用了传感中包含的信息,同时利用了沿病态条件方向的外部信息
所提出的框架在不同环境和感官条件下的多个现实世界任务中进行了广泛的测试,现实世界的实验和分析表明,该框架可以在各种环境条件下可靠地检测可定位性,而无需根据具体情况调整参数,并且在退化环境下具有较高的鲁棒性和准确性。在具有挑战性和部分退化的场景中进行的所有实验中,所提出的框架始终优于最先进的机器人方法15,24,参见图1中类似隧道环境的示例。
因此,本文的主要贡献为:
- 一种多层次、鲁棒用于scan-to-map配准的可定位性检测算法的开发与集成。为了研究多级探测的效果,我们进行了详细的消融研究
- 开发了一种新的可定位性考量约束ICP优化模块,并与可定位性检测紧密耦合以减轻退化的影响
- 进行了各种实验来评估所提出的框架的有效性,并将结果与最先进的方法进行比较。此外,还提供了附加内容、数据和补充材料
相关工作
退化检测
点云建图中的约束优化
约束优化技术在文献中是众所周知的;然而,它们在点云配准中的应用最近才引起人们的关注。首先,[51]提出了一种无穿透点云配准的约束优化方法,提高了姿态估计的质量。类似地,[52]使用非线性等式约束来减少点云配准中旋转估计的线性化误差。为了提高对传感器噪声和对应异常值的鲁棒性,[53]提出通过将每个测量作为单独的约束添加,使用增广拉格朗日来解决约束优化问题。最近的一项研究54引入了软约束作为ICP优化的成本,以确保不同扫描之间的轨迹连续性。
相比之下,55将点云配准问题表述为约束二次规划,以提供全局最优的点云配准结果
这些方法提高了全局点云配准问题的鲁棒性和准确性;然而,他们没有解决约束的效用,以限制优化中的退化的影响。为了解决这一挑战,并且与所提出的方法最相关,44提出使用相对条件数来检测退化性,并通过在因子图公式中引入约束来惩罚沿退化方向的运动变化
据作者所知,这方面的研究只有44。然而,这项工作仅限于2D导航,并没有考虑在低级ICP优化中使用这些约束,鉴于上述讨论,使用退化分析来约束机器人在具有挑战性和退化的环境中操作的ICP注册问题仍然是一个开放的问题,本工作旨在解决这个问题。
问题描述
受先前研究结果的启发,本工作提出了一种在几何挑战性和退化环境中进行机器人姿态估计和可靠点云配准的解决方案。仅利用LiDAR点云和外部里程计估计作为输入,并将该方案分为可定位性检测和约束点云配准两部分。所提出的组件可以在计算资源有限的机器人系统上实时运行。
问题形成
点云配准
点云配准问题定义为寻找一个刚体变换\(\boldsymbol{T}_{\mathrm{ML}} \in S E(3)\),该刚体变换能够将LiDAR坐标系中\(N_p\)个点\({ }_{\mathrm{L}} \boldsymbol{P} \in \mathbb{R}^{3 \times N_p}\)的点云(记为L)与地图框架中\(N_q\)点,\({ }_{\mathrm{M}} \boldsymbol{Q} \in \mathbb{R}^{3 \times N_q}\)的参考点云(记为M)进行最佳对齐。
刚体变换\(\boldsymbol{T}_{\mathrm{ML}} \in S E(3)\)由旋转和平移组成,对于LiDAR坐标系中的每个点,地图中的参考点通常通过kd-tree进行搜索找到,这个数据关联的过程记为:\(\mathcal{M} \in \mathbb{R}^{6 \times N}=\operatorname{matching}\left({ }_{\mathrm{L}} \boldsymbol{P},{ }_{\mathrm{m}} \boldsymbol{Q}, \boldsymbol{T}_{\mathrm{LM}, \text { init }}\right)=\left.\left\{\left({ }_{\mathrm{M}} \boldsymbol{p},\left \{ { }_{\mathrm{M}} \boldsymbol{q},{ }_{\mathrm{M}} \boldsymbol{p}\right\}\right):\left({ }_{\mathrm{M}} \boldsymbol{p} \in{ }_{\mathrm{M}} \boldsymbol{P}\right),{ }_{\mathrm{M}} \boldsymbol{q} \in{ }_{\mathrm{M}} \boldsymbol{Q}\right)\right\}\),其中\({ }_{\mathrm{M}} \boldsymbol{p}\) 和 \({ }_{\mathrm{M}} \boldsymbol{q}\)是匹配点对,\({ }_{\mathrm{M}} \boldsymbol{n} \in \mathbb{R}^3,\left\|_{\mathrm{M}} \boldsymbol{n}\right\|=1\)是\(_M\boldsymbol{q}\)的平面法向量。
另外,N≤Np是匹配点的个数,表示接下来的工作的问题大小。初始变换\(\boldsymbol{T}_{\text {LM,init }}\)通常作为初始猜测提供,将扫描数据转换为参考坐标系,以改善匹配过程和优化收敛特性。虽然这种初始转换的准确性对于最小化的收敛至关重要[14],但这种初始转换的质量的影响不在本工作的范围内。
定义点云对齐误差函数有多种方法;在本工作中,将使用点到平面[7]的代价函数。具有点到平面成本函数的ICP最小化问题定义如下:

不同的求解方法,如奇异值分解(SVD)[56]、LU分解、Gauss-Newton和Levenberg-Marquardt,都可以用来求解这个最小化问题。在这项工作中,重点是直接线性代数求解器,如SVD,它直接以矩阵形式运算。
根据Pomerleau等人[57]的推导,引入标量三重积和旋转矩阵线性化,最小化(1)可以重新表述为二次代价优化问题,如下:
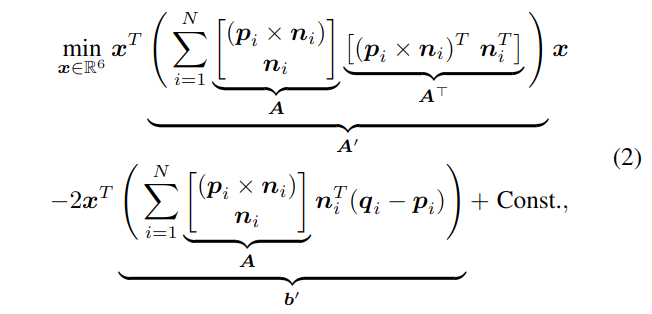
其中,
- \(\boldsymbol{x}=\left[\boldsymbol{r}^{\top} \boldsymbol{t}^{\top}\right]^{\top} \quad \in \mathbb{R}^6\)是待优化变量
- \(\boldsymbol{r} \in \mathfrak{s o}(3)\)是李代数SO3的旋转量
- \(\boldsymbol{t} \in \mathbb{R}^3\)
- \(\boldsymbol{A}^{\prime} \in \mathbb{R}^{6 \times 6}\)为优化问题的Hessian矩阵
- \(\boldsymbol{b}^{\prime} \in \mathbb{R}^6\)结合点云之间的约束
- 此公式(2)中的\(\boldsymbol{p}_i\)应该是根据位姿初值投影到地图坐标系后的投影点坐标
Hessian构成了优化的二阶矩矩阵,并定义了雅可比矩阵的局部行为。并且,式(2)是众所周知的以优化变量\(x\)为变量的二次最小化形式,可以将其重新表述为正则最小二乘优化公式如下:
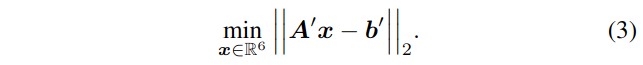
对于(半)正定矩阵\(\boldsymbol{A}^{\prime}\),求解这个最小化问题很简单。该6 × 6线性方程组的解将得到在该线性化点下的最优平移矢量\(\boldsymbol{t}\)和旋转矢量\(\boldsymbol{r}\)。在ICP过程中,由于非线性和由此产生的算法的迭代性质,这里描述的这些操作被重复,直到收敛。
在退化环境中的操作
在实际应用中,由于缺乏几何信息结构而引起的环境退化,上述点云配准可能会失败。之前的配准的解\(\boldsymbol{T}_{\mathrm{ML}}\)是欠约束的,这意味着6-DoF变换的一个或多个维度(几乎)不能从观测到的correspondences中观察到。
因此,本工作试图解决的主要问题被定义为在存在环境退化的情况下找到最佳转换\(\boldsymbol{T}_{\mathrm{ML}}\),同时确定由于欠约束导致的难以估计的方向。
虽然在大多数先前的工作中忽略了这一点,但这项工作提出了一个专门针对这些情况的解决方案,以便在极端情况下运行。
系统概览
所提出系统的概述如图2所示。提出了一种检测和减轻退化的新组件Loc.-Module和Opt.-Module,嵌入到scan-to-map配准系统Pharos[58],[59],由ANYbotics开发。但是,值得注意的是,所提出的组件可以集成到任何基于迭代优化的配准方法中。Pharos以5hz的频率运行,并与著名的点云配准库libpointmatcher的点对平面ICP实现紧密耦合[59]。此外,Pharos利用外部里程计姿态估计来补偿点云畸变,并作为配准先验\(\boldsymbol{T}_{\mathrm{ML}, \text { init }}\),实现scan-to-map的关联搜索。
可定位性检测模块概述
Loc.-Module的目标是近似于ICP优化的Hessian \(\boldsymbol{A}^{\prime}\)的零空间。为了实现这一目标,引入了一个跨越6自由度优化问题的可定位性向量。这个局部化向量指示哪些特征向量在或应该被考虑为Hessian零空间内。可定位性向量定义为:

其中,\(\left \{ { }_{\mathrm{L}} \boldsymbol{v}_{t_1}, \mathrm{~L}_{\mathrm{L}} \boldsymbol{v}_{t_2},{ }_{\mathrm{L}} \boldsymbol{v}_{t_3}\right\} \in \boldsymbol{V}_t\)是Hessian \(\boldsymbol{A}^{\prime}\)关于变量\(t\)的平移特征向量(在雷达坐标系下的表示),相似的,\(\left \{ { }_{\mathrm{L}} \boldsymbol{v}_{r_1,{ }_{\mathrm{L}}} \boldsymbol{v}_{r_2, \mathrm{~L}_{\mathrm{L}}} \boldsymbol{v}_{r_3}\right \} \in \boldsymbol{V}_r\)只对应于旋转向量\(\boldsymbol{r}\)。
重要的是,如第II-A节所讨论的,ICP的雅可比矩阵由两个独立的元素组成,分别是平移和旋转的\(\boldsymbol{n}\)和\(\boldsymbol{p} \times \boldsymbol{n}\),这是点对平面成本函数的固有属性。为了保持这一性质的有效性,在本工作中,在可定位性分析中省略了平移分量和旋转分量之间的交叉协方差。因此,只需要平移和旋转特征向量。
关于如何获得\(\boldsymbol{V}_t\) 和 \(\boldsymbol{V}_r\)的更多细节将在第V节的步骤V- a中解释。可定位性类别\(\Omega\)以分类变量的形式表示每个特征向量的可局部化状态;这个离散的可本地化空间定义为\(\boldsymbol{\Omega}_i \in \{none, partial, full \}\),其中的类别分别对应于不可定位、部分可定位和可定位。每个类别的操作顺序将在第V节的步骤V- c中解释。
考量可定位性的优化模块概述
利用Loc.-Module模块的输出,如可定位性类别\(\Omega\),Opt.-Module的目标定义为构造和求解包含约束的优化问题,该问题将用于寻找优化问题(3)的最优解\(\boldsymbol{x}^*\)。这一过程将在章节VI. 中详细说明。在这一部分中,使用基于拉格朗日乘子的约束优化技术来获得给定观察到的局部性的最优可能解。
可定位性检测模块
在本节中,将详细介绍Loc.-Module按照图3所示的信息流进行描述。可定位性检测的目的是分析关联数据中的信息,从而正确识别约束不足的方向。如图3所示,给定关联数据关系,第一个任务是信息分析,分析Hessian与来自环境的几何信息之间的关系。第二步,“过滤”,过滤掉第一步中信息分析步骤中的冗余信息。最后,对过滤后的信息进行解释,从而实现细粒度分类。经过关联数据搜索后,将匹配的关联变换回LiDAR坐标系\(\mathrm{L}\),消除地图物理尺寸的影响,并在该帧中进行可定位性分析
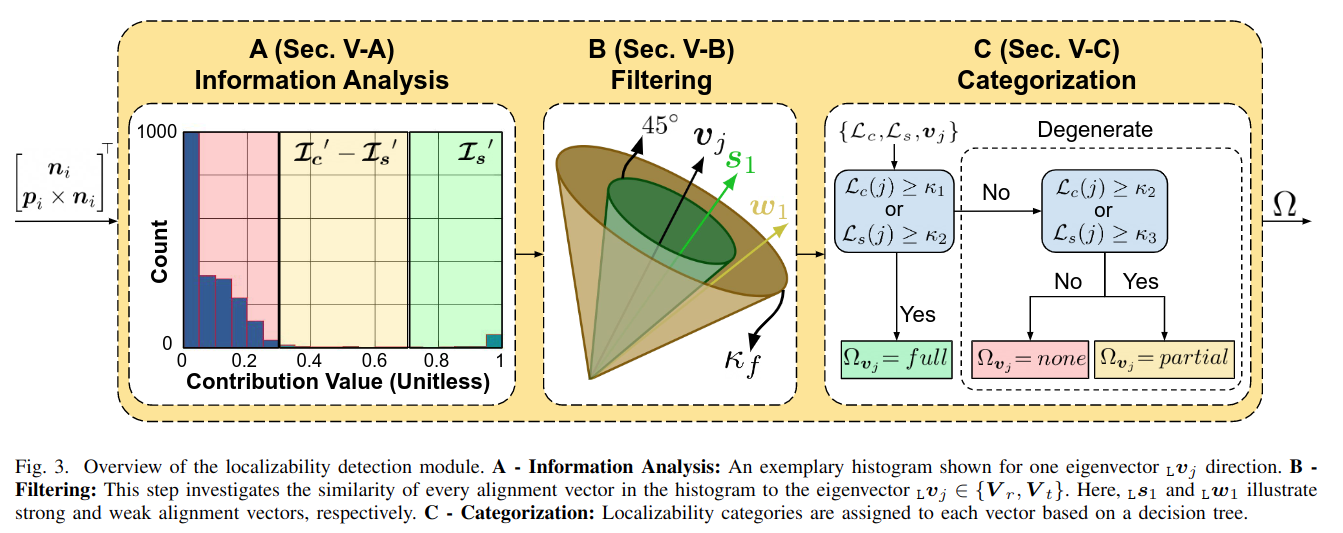
信息分析
Eigenanalysis
信息分析从优化问题的Hessian矩阵的特征分析开始。对于点到面ICP成本函数矩阵的推导,请参考第IV节,其中Hessian为式(3)中的\(A^{\prime}\)。根据待优化的变量\(\boldsymbol{x}\)的含义,Hessian可以划分为子矩阵:

这里,\(\boldsymbol{A}_{r r}^{\prime} \in \mathbb{R}^{3 \times 3}\)只包含与旋转变量相关的信息。同样,\(\boldsymbol{A}_{t t}^{\prime} \in \mathbb{R}^{3 \times 3}\)只包含与平移变量相关的信息。
利用奇异值分解(SVD)对\(\boldsymbol{A}_{t t}^{\prime} \in \mathbb{R}^{3 \times 3}\)和\(\boldsymbol{A}_{r r}^{\prime} \in \mathbb{R}^{3 \times 3}\)进行特征分析。对于旋转和平移分量,特征分解为:
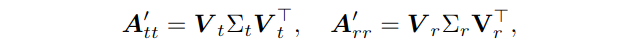
其中\(\boldsymbol{V}_t \in S O(3)\) 和 \(\boldsymbol{V}_r \in S O(3)\)是矩阵形式的特征向量。\(\Sigma_t \in\left\{\operatorname{diag}(\boldsymbol{v}): \boldsymbol{v} \in \mathbb{R}^n{\geq 0}\right\}\) 和 \(\Sigma_r \in\left\{\operatorname{diag}(\boldsymbol{v}): \boldsymbol{v} \in \mathbb{R}^n{\geq 0}\right\}\)分别是以\(\boldsymbol{A}_{t t}^{\prime} \in \mathbb{R}^{3 \times 3}\)和\(\boldsymbol{A}_{r r}^{\prime} \in \mathbb{R}^{3 \times 3}\)的特征值为对角项的对角矩阵。
有趣的是,\(\Sigma_t\) 和 \(\Sigma_r\)中的特征值提供了与其配对的每个特征向量的信息的直接度量。然而,正如第II节所讨论的,特征值对于不同的环境和传感器可能表现不一致,因此不直接用于本工作的可定位性估计。
Information Pair Contribution
信息分析的第二部分是制定每个数据关联对的贡献,定义为\(\left({ }_{\mathrm{L}} \boldsymbol{p},{ }_{\mathrm{L}} \boldsymbol{n}\right)\)。需要在数据关联对和成本之间建立正式的关系,以评估数据关联对对成本的贡献。与其他作品[38]、[39]、[60]相似,本文选择优化的雅可比矩阵作为贡献指标。
可以直观地看到,式(2)中定义的雅可比矩阵A,根据定义度量了优化变量\(\boldsymbol{X}_i\)的代价变化。
Analogy to Classical Mechanics
与经典力学类似,雅可比矩阵测量由每个数据关联对局部引起的影响的大小。 一个扳手系统由力和扭矩组成:在给出的应用中,可以认为这对作用力和扭矩作用于解\(\boldsymbol{x}\),在本例中,对解进行平移的力定义为表面法向量\(n\),对解进行旋转的扭矩定义为\(\boldsymbol{\tau}=\boldsymbol{p} \times \boldsymbol{n}\)。虽然直观,扭矩公式不提供一个可推广的参数化在其简单的形式。点\(p\)可以处于不同的距离,导致更远点的扭矩更高,这阻碍了该公式在实际应用中的推广。
Kwok和Tang[39]研究了这种尺度差异对不同归一化技术的ICP算法的影响。研究表明,最大规范归一化比平均规范归一化表现更好,如[38]或矩归一化所做的那样。
这对于可靠地解决ICP问题是正确的,其中需要点之间的空间关系。然而,对于局部化估计的逐点贡献计算,情况并非如此。考虑到这一事实以及点范数不应直接影响贡献值的要求,本工作提出使用矩归一化,将扭矩值映射到单位球(如式(5)所示)。
Information Matrix
为了数值稳定性,如果\(|\boldsymbol{\tau}|\)接近于零(即,向量接近平行),信息对被丢弃,(这发生在平面法向量直接指向传感器坐标系) 【此处个人感觉描述有误,这应该发生在平面法向量与关联点与世界坐标系原点的连线平行的时候,叉乘为0】。
此外,矩归一化仅适用于\(|\boldsymbol{\tau}| \geq 1\)的信息对,防止转矩值在单位球内的映射,因为这可能会推动Loc.-Module走向乐观可定位性检测。
在转矩向量的矩归一化之后,将扳手系统堆叠为所有可用的信息对,形成如下信息矩阵:

其中,
- \(\mathcal{F}_r \in \mathbb{R}^{N \times 3}\) 和 \(\mathcal{F}_t \in \mathbb{R}^{N \times 3}\)分别是旋转和平移信息矩阵
信息分析的最后一个任务是从\(\mathcal{F}_r \in \mathbb{R}^{N \times 3}\) 和 \(\mathcal{F}_t \in \mathbb{R}^{N \times 3}\)计算可定位性贡献
Localizability Contributions
可定位性概念在每个特征值的特征空间中定义,因此,对于每个特征向量方向都可以得到,这确保了检测不会受到激光雷达或机器人在环境中的朝向的影响,这是实际应用中的一个关键优势。因此,等式 (5) 中定义的信息矩阵被投影到平移和旋转 Hessian 的特征空间中。为了实现这一点,特征向量矩阵\(\mathbf{V}_r\) 和 \(\mathbf{V}_t\)将按如下方式使用:

其中,
- \(\mathcal{I}_r, \mathcal{I}_t \in \mathbb{R}^{N \times 3}\)是所有数据关联对\(\{ \boldsymbol{p}, \boldsymbol{n} \}\)的可定位性贡献,经过\(\left \{ \mathbf{V}_r, \mathbf{V}_r\right \}\)中的特征向量投影
- \((\ldots)^{|\cdot|}\)操作符表示向量的每个元素绝对值
- 同时,\(\mathcal{I}_r\) 和 \(\mathcal{I}_t\)中的标量值是某一方向可定位性贡献的直接指标
如果标量值为\(\mathcal{I}(i)=1.0\),则方向的局部性贡献是完美的,如果\(\mathcal{I}(i)=0.0\),则数据关联对对这个方向的可定位性没有贡献。
过滤
给定等式 (6) 中定义的可实现性贡献\(\mathcal{I}=\left[\mathcal{I}_r, \mathcal{I}_t\right] \in \mathbb{R}^{N \times 6}\),过滤步骤的目标是删除冗余信息并使当前信息可解释。
Filtering Low Contribution
冗余信息示例如图 3-A 所示,其中红色突出显示的低贡献区域主导了分析,如果可定位性的贡献较小,则可能与测量噪声或特征提取噪声无法区分。此步骤通过使用二进制元素过滤来解决这个问题。过滤操作是一个重新分配操作,定义如下:
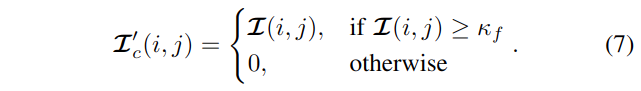
其中,
- 这里的索引定义为\(i \in\{1, \ldots, N\}\) 和 \(j \in \{1, \ldots, 6\}\),
- \(\mathcal{I}_c{ }^{\prime}\)是过滤后的可定位性贡献向量,它包含所有可靠的可定位性贡献值
- 此外,\(\kappa_f\)是过滤参数,第一个用户定义的参数。由于该参数捕获不同激光雷达传感器的传感器和特征提取噪声,因此应根据传感器和特征提取进行重新调整
除Ouster OS0-128外,该参数在所有实验中设置为\(\kappa_f=\cos \left(80^{\circ}\right) \approx 0.1736\),考虑到Ouster OS0-128与Velodyne VLP-16相比不同的噪声特性;Ouster LiDAR 测量受到更高的方差的影响,因此,设置为\(\kappa_f = \cos \left(60^{\circ}\right)=0.5\)以实现更积极的过滤。
Filtering High Contribution
使用这种过滤后的可本地化贡献\(\mathcal{I}_c^{\prime}\)(大于阈值\(\kappa_f\) 的贡献),可以结合起来总结可用的几何信息:

其中,
- \(\mathcal{L}_c \in \mathbb{R}^{1 \times 6}\)是所有可靠数据关联对的可定位性的贡献求和后的向量。
更多的对应关系表明可用的信息更高。同时,更多的对应关系还包括更多的传感器和特征提取噪声。V-B1 节的过滤步骤充当异常值拒绝步骤,并有助于减少这些影响。矩阵 \(\mathcal{I}_{\boldsymbol{c}}{ }^{\prime}\) 仍然包含弱但可靠的贡献,需要保留。
然而,仍然需要衡量最强的贡献来识别可定位性更细粒度的状态,这个过滤步骤基于几何向量对齐;只有大于\(\cos \left(45^{\circ}\right) \approx 0.707\)的对齐值才会被认为是强有力的贡献,通过几何关系证明。在图 3-B 中,可视化了强对齐区域和弱对齐区域与特征向量的分离。内绿色锥表示向量对齐强的区域,黄色区域表示弱区域。这种分离公式如下:
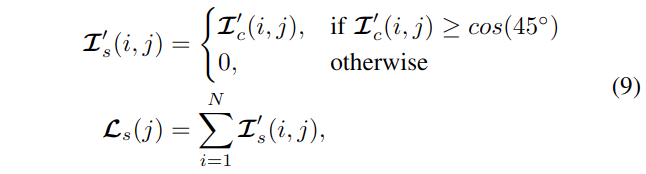
其中,
- \(\mathcal{L}_s \in \mathbb{R}^{1 \times 6}\)是是强可定位性的贡献向量。与组合可定位性贡献\(\mathcal{L}_c(j)\)类似,该表达式也受到 N 变化的影响,但是它对传感器噪声不太敏感,仅受特征提取误差的影响
这些强可定位性的贡献向量\(\mathcal{L}_s\)和组合可定位性贡献向量\(\mathcal{L}_c\)对于下一步至关重要,其中这些向量将用于对可定位性进行分类
Categorization
Loc.-Module的最后一步将根据上一步的信息,提供了可定位性分类
可定位性参数
为了实现这一目标,引入了三个可定位性参数:
- 参数\(\kappa_1\)是定义完全可定位的下界的安全可定位阈值
- 参数\(\kappa_2\)调节从可定位到部分可定位的转换,并表示部分可定位的阈值上限
- 参数\(\kappa_3\)是最小信息阈值,涵盖了环境稀疏但对齐良好的信息的情况,并调节从部分可定位到不可定位的转换。
参数选择
这些阈值的定义提供了参数之间的自然界限,\(\kappa_1 \geq \kappa_2>\kappa_3\)。这些参数是根据所采用的ICP算法的收敛范围来设置的。
参数设置规则如下:
- 由于\(\kappa_1\)设置了可本地化和{partial-localizability, non-localizable}之间的边界,它可以设置为任意高。唯一的缺点是可定位性检测的计算成本,一个示例:\(\kappa_1 = 500\)表示ICP优化运行至少500个完美的匹配对。
- 另一方面,设置\(\kappa_2\)是一种系统特性选择。它与\(\kappa_3\)共同定义了如何处理局部可定位性。它应该设置在\(\kappa_1\)和\(\kappa_3\)之间。
- 最后,\(\kappa_3\)设置了部分可定位和不可定位状态的边界。值为50表明允许约束ICP优化以最少50个采样对的受控方式运行
利用这些直觉,在本工作的其余部分,将第7节中所有环境和传感器的可定位性参数设置为\(\kappa_1= 250\), \(\kappa_2 = 180\)和\(\kappa_3 = 35\)。
### 决策树
在决策树中使用这些参数来获得如图3-C所示的可定位性类别。决策树以过滤后的可定位性贡献向量和特征向量作为输入。决策树按特征向量操作;因此,对所有6个方向重复所需的二进制比较。
首先,通过比较\(\kappa_1\) 与\(\mathcal{L}_c\)、\(\kappa_2\) 与\(\mathcal{L}_s\),验证优化问题是否在特征向量方向上可解。如果这些比较中的任何一个表明问题是良好约束的,那么该方向是可定位的,\(\Omega_{\boldsymbol{v}_j}=\) full.。
其次,假设第一步的比较表明问题没有很好的约束;在这种情况下,将\(\kappa_2\)与\(\mathcal{L}_c\)进行比较,将\(\kappa_3\)与\(\mathcal{L}_s\)进行比较,以了解优化问题中是否存在可挽救的信息。
如果这些比较中的任何一个成立,可定位性类别被分配为partial,即部分可定位, \(\Omega_{\boldsymbol{v}_j}=\) partial,否则,则表示是不可定位\(\Omega_{\boldsymbol{v}_j}=\) none
### Xs-ICP - Simplified X-ICP
...
# 考虑可定位性的优化模块